Advertisements
Advertisements
प्रश्न
एक बहुफलकी में 60 किनारे और 40 शीर्ष हैं। उसके फलकों की संख्या ज्ञात कीजिए।
उत्तर
बहुफलक के लिए ऑयलर के सूत्र का उपयोग करके,
F + V – E = 2 ...[जहाँ, F = फलक, V = शीर्ष, E = किनारा]
⇒ F + 40 – 60 = 2 ...[∵ E = 60 और V = 40, दिया गया है।]
⇒ F – 20 = 2
⇒ F = 2 + 20
⇒ F = 22
अतः, फलकों की संख्या 22 है।
APPEARS IN
संबंधित प्रश्न
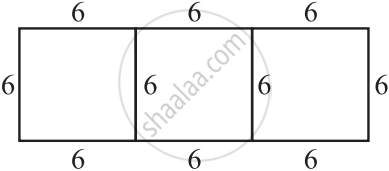
यहाँ एक घन बनाने के लिए, एक अधूरा जाल दिया गया है। इसको कम-से-कम दो विधियों से पूरा कीजिए। याद रखिए कि घन के 6 फलक होते हैं। यहाँ इस जाल में कितने फलक दिए हुए हैं (दो पृथक्-पृथक् चित्र दीजिए।) कार्य को सरल बनाने के लिए आप वर्गांकित कागज का प्रयोग कर सकते हैं।
एक वर्गाकार कागज़ की मदद से बुधा घन बनाना चाहता है। वह जनता है कि घन की हर सतह वर्ग होती है।
वह दो अलग-अलग आकृतियाँ बनाता है।
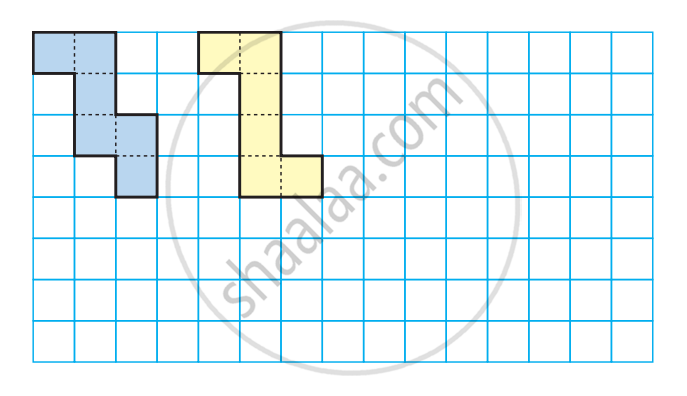
क्या ये दोनों आकृतियाँ मुड़ने पर एक घन बना सकती हैं?
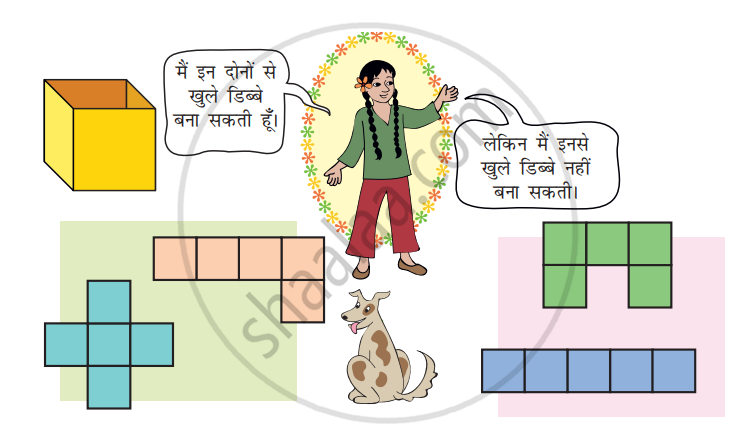
- बनाकर पता लगाओ कि पेज 46 की बाकी 8 आकृतियों में कौन सी हैं जिनको मोड़ कर एक खुला डिब्बा बनाया जा सकता है।
आकृति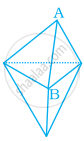 
में, B पर मिलने वाले फलकों की संख्या ______ है।
एक बहुफलकी में तीन फलक हो सकते हैं।
एक घनाभ के न्यूनतम 4 विकर्ण होते हैं।
निम्नलिखित ठोस में कितने फलक हैं?
अष्ठभुजाकार पिरामिड
निम्नलिखित ठोस में कितने किनारे हैं?
केलिडस्कोप
नीचे दिये गए आकार में फलकों की संख्या ज्ञात कीजिए-
नीचे दिये गए आकार में फलकों की संख्या ज्ञात कीजिए-
