Advertisements
Advertisements
प्रश्न
एक प्रदर्शनी हॉल में 24 प्रदर्शनी पट्ट (display board) हैं। जिनमें से प्रत्येक पट्ट 1 m 50 cm व लंबा 1 m चौड़ा है। इन पट्टों के चारों ओर फ्रेम लगाने के लिए 100 m लंबी एल्यूमीनियम की पट्टी है। इस पट्टी का प्रयोग करते हुए कितने पट्टों को फ्रेम किया जा सकता है? शेष बचे हुए पट्टों के लिए आवश्यक एल्यूमिनियम पट्टी की लंबाई भी ज्ञात कीजिए।
उत्तर
दिया गया है, कुल प्रदर्शनी पट्ट = 24
एक प्रदर्शनी पट्ट की लंबाई = 1 m + 50 cm = 1 m + `50/100` m ......[∵ 1 m = 100 cm]
= (1 + 0.5) m
= 1.5 m
एक प्रदर्शनी पट्ट की चौड़ाई = 1 m
∴ एक प्रदर्शनी पट्ट का परिमाप = 2 × (लंबाई + चौड़ाई)
= 2 × (1.5 + 1) m
= 2 × 2.5 m
= 5 m
पट्टी की लंबाई = 100 m ......[दिया गया]
अब, पट्ट की संख्या तैयार की जाएगी = `"पट्टी की लंबाई"/"एक पट्टी की परिधि"`
= `100/5`
= 20
यानी 24 में से 20 पट्टी ही बनेंगे।
बिना फ्रेम के बचे पट्ट की संख्या = `24 - 20` = 4
∴ शेष पट्ट के लिए आवश्यक पट्टी की लंबाई = 4 × एक पट्ट का परिमाप
= 4 × 2(1.5 + 1)
= 4 × 2 × 2.5
= 20 m
APPEARS IN
संबंधित प्रश्न
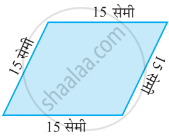
नीचे दी हुई आकृति का परिमाप ज्ञात कीजिए:
एक मेज़ की ऊपरी सतह की विमाएँ 2 मी 25 सेमी और 1 मी 50 सेमी हैं। मेज़ की ऊपरी सतह का परिमाप ज्ञात कीजिए।
निम्न आकृति का परिमाप ज्ञात कीजिए:
एक त्रिभुज जिसकी भुजाएँ 3 सेमी, 4 सेमी और 5 सेमी हैं।
निम्न आकृति का परिमाप ज्ञात कीजिए:
एक समद्विबाहु त्रिभुज जिसकी प्रत्येक समान भुजाएँ 8 सेमी की हो और तीसरी भुजा 6 सेमी हो।
एक आयताकार मैदान की लंबाई उसकी चौड़ाई की तीन गुना है। यदि इसमै दान का परिमाप 800 m है तो मैदान की लंबाई कया है?
निम्नलिखित आकृतियाँ छः इकाई वर्गों को जोड़कर बनी हैं। किस आकृति का परिमाप न्यूनतम है?
एकसम अष्टभुज जिसकी भुजा 6 cm है, का परिमाप 36 cm है।
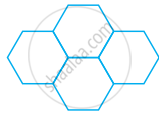
चार समषट्भुज, जिनमें प्रत्येक की भुजा की लंबाई समान है। आकृति में दर्शाए गये डिजाइन के अनुसार बनाए गये हैं। यदि डिजाइन का परिमाप 28 cm हो तो एक षट्भुज की प्रत्येक भुजा की लंबाई ज्ञात कीजिए।
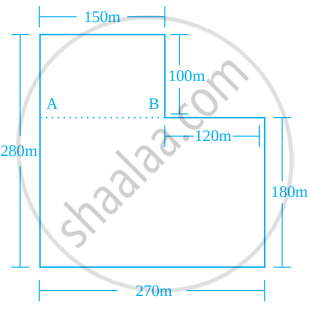
आकृति में दिखाए गए पार्क की बाड़ लगाने का कुल खर्च 55000 रु है। बाड़ लगाने की प्रति वर्गमीटर दर ज्ञात कीजिए।
एक आयताकार मैदान की लंबाई, चौड़ाई की 6 गुना है। यदि मैदान की लंबाई 120 cm हो तो इसकी चौड़ाई और परिमाप ज्ञात कीजिए।
