Advertisements
Advertisements
प्रश्न
एक टाकी दोन नळांच्या साहाय्याने 2 तासांत पूर्ण भरते. त्यातील फक्त लहान नळाने टाकी भरण्यास लागणारा वेळ, फक्त मोठ्या नळाने टाकी भरण्यास लागणाऱ्या वेळेपेक्षा 3 तास जास्त असतो, तर प्रत्येक नळाने ती टाकी भरण्यास किती वेळ लागतो?
उत्तर
समजा, मोठ्या नळाने टाकी भरण्यास x तास लागतात.
∴ मोठ्या नळाने 1 तासात `1/x` इतकी टाकी भरेल.
तसेच, लहान नळाने टाकी भरण्यास लागणारा वेळ = (x + 3) तास
∴ लहान नळाने 1 तासात `1/(x + 3)` इतकी टाकी भरेल.
∴ एका तासात दोन्ही नळांनी भरला जाणारा टाकीचा भाग
`= (1/x + 1/(x + 3))`
परंतु, टाकी दोन्ही नळांच्या साहाय्याने 2 तासांत पूर्ण भरते.
∴ एका तासात टाकी दोन्ही नळांनी `1/2` इतकी भरेल.
दिलेल्या अटीनुसार,
`1/x + 1/(x + 3) = 1/2`
∴ `(x + 3 + x)/(x(x + 3)) = 1/2`
∴ `(2x + 3)/(x(x + 3)) = 1/2`
∴ 2(2x + 3) = x(x + 3)
∴ 4x + 6 = x2 + 3x
∴ x2 + 3x - 4x - 6 = 0 ...`[(-6= -3; 2),(- 3 xx 2 = - 6),(- 3 + 2 = - 1)]`
∴ x2 - x - 6 = 0
∴ x2 - 3x + 2x - 6 = 0
∴ x(x – 3) + 2(x – 3) = 0
∴ (x – 3)(x + 2) = 0
जर दोन संख्यांचा गुणाकार शून्य असेल, तर त्या दोन संख्यांपैकी किमान एक संख्या शून्य असते, या गुणधर्माच्या उपयोजनाने
∴ x - 3 = 0 किंवा x + 2 = 0
∴ x = 3 किंवा x = - 2
परंतु, वेळ कधीही ऋण नसते.
∴ x = 3 आणि x + 3 = 3 + 3 = 6
∴ मोठ्या नळाने टाकी भरण्यास 3 तास आणि लहान नळाने टाकी भरण्यास 6 तास लागतील.
APPEARS IN
संबंधित प्रश्न
विवेक, हा किशोरपेक्षा 5 वर्षांनी मोठा असून त्यांच्या वयांच्या गुणाकार व्यस्तांची बेरीज `1/6` आहे, तर त्यांची आजची वये काढा.
श्री. मधुसूदन यांच्या संत्राबागेत आडव्या रांगेतील झाडांची संख्या, उभ्या रांगेतील झाडांच्या संख्येपेक्षा 5 ने अधिक आहे. जर संत्राबागेत एकूण 150 झाडे असतील, तर आडव्या तसेच उभ्या रांगेतील झाडांची संख्या किती? खालील प्रवाहआकृतीच्या आधारे उदाहरण सोडवा.

सुयशला गणिताच्या पहिल्या चाचणीत मिळालेल्या गुणांपेक्षा दुसऱ्या चाचणीत 10 गुण अधिक मिळाले. दुसऱ्या चाचणीतील गुणांची 5 पट ही पहिल्या चाचणीतील गुणांच्या वर्गाइतकी आहे, तर त्याचे पहिल्या चाचणीतील गुण किती?
पिंटूला एक काम करण्यासाठी निशूपेक्षा ६ दिवस अधिक लागतात. दोघांनी मिळून काम केल्यास ते काम पूर्ण करण्यासाठी त्यांना ४ दिवस लागतात, तर ते काम एकट्यानेच पूर्ण करण्यास प्रत्येकास किती दिवस लागतील?
समलंब मध्ये `square`ABCD मध्ये AB || CD असून त्याचे क्षेत्रफळ 33 चौसेमी आहे, तर आकृतीतील दिलेल्या माहितीवरून चौकोनाच्या चारही बाजूंची लांबी खालील कृती पूर्ण करून काढा.
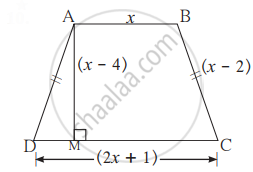
उकल:
`square`ABCD समलंब चौकोन आहे. AB || CD
`"A"(square "ABCD") = 1/2 xx ("AB" + "CD") xx square`
∴ `33 = 1/2(x + 2x + 1) xx square`
∴ `square` = (3x + 1) × `square`
∴ 3x2 + `square` - `square` = 0
∴ 3x (____) + 10 (____) = 0
∴ (3x + 10)(_____) = 0
∴ (3x + 10) = 0 किंवा `square` = 0
∴ x = `- 10/3` किंवा x = `square`
परंतु, लांबी ऋण नसते.
∴ `x ne (- 10)/3` ∴ x = `square`
AB = ______, CD = ______, AD = BC = _______
मुकुंदजवळ सागरपेक्षा 50 रुपये अधिक आहेत. त्यांच्याजवळील रकमांचा गुणाकार 15,000 असेल, तर प्रत्येकाजवळील रक्कम किती?
दोन संख्यांच्या वर्गांमधील फरक 120 आहे. लहान संख्येचा वर्ग हा मोठ्या संख्येच्या दुपटीइतका आहे, तर त्या संख्या शोधा.
तळवेल येथील शेतकरी श्री. दिनेश यांच्या आयताकृती शेतीची लांबी ही रुंदीच्या दुपटीपेक्षा 10 मीटरने अधिक आहे. त्यांनी त्या शेतात पावसाचे पाणी पुनर्भरणासाठी शेताच्या रुंदीच्या `1/3` पट बाजू असणाऱ्या चौरसाकृती शेततळ्याची निर्मिती केली. तेव्हा मूळ शेताचे क्षेत्रफळ हे शेततळ्याच्या क्षेत्रफळाच्या 20 पट होते, तर त्या शेताची लांबी आणि रुंदी, तसेच शेततळ्याच्या बाजूची लांबी काढा.
खालील शाब्दिक उदाहरण सोडवण्यासाठी कृती पूर्ण करा.
दोन क्रमागत सम नैसर्गिक संख्यांच्या वर्गांची बेरीज 244 आहे, तर त्या संख्या शोधा.
कृती: पहिली सम नैसर्गिक संख्या x मानू.
दुसरी क्रमागत सम नैसर्गिक संख्या = (______)
दिलेल्या अटीनुसार,
x2 + (x + 2)2 = 244
x2 + x2 + 4x + 4 – (______) = 0
2x2 + 4x – 240 = 0
x2 + 2x – 120 = 0
x2 + (______) – (______) – 120 = 0
x (x + 12) – (______) (x + 12) = 0
(x + 12) (x – 10) = 0
x = (______) / x = 10
परंतु, नैसर्गिक संख्या ऋण नसते, म्हणून x = -12 शक्य नाही.
म्हणून, पहिली नैसर्गिक संख्या x = 10 असेल.
म्हणून, दुसरी नैसर्गिक संख्या = x + 2 = 10 + 2 = 12 असेल.
एका बागेत 200 झाडे असून प्रत्येक रांगेतील झाडांची संख्या ओळीच्या संख्येपेक्षा 10 ने जास्त आहे, तर प्रत्येक रांगेतील झाडांची संख्या काढा.
