Advertisements
Advertisements
प्रश्न
Explain in detail Newton’s law of cooling.
उत्तर
Newton’s law of cooling: Newton’s law of cooling states that the rate of loss of heat of a body is directly proportional to the difference in the temperature between that body and its surroundings.
`"dQ"/"dt" ∝ ("T" - "T"_"s")` ............(1)
The negative sign indicates that the quantity of heat lost by liquid goes on decreasing with time. Where,
T = Temperature of the object
Ts = Temperature of the surrounding
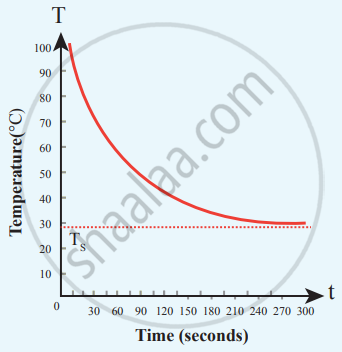
Cooling of hot water with time
From the graph in the figure, it is clear that the rate of cooling is high initially and decreases with falling temperature.
Let us consider an object of mass m and specific heat capacity s at temperature T. Let Ts be the temperature of the surroundings. If the temperature falls by a small amount dT in time dt, then the amount of heat lost is,
dQ = msdT .........(2)
Dividing both sides of equation (2) by dt
`"dQ"/"dt" = "msd"/"dt"` .........(3)
From Newton’s law of cooling `"dQ"/"dt" ∝ ("T" - "T"_"s")`
`"dQ"/"dt" = - "a"("T" - "T"_"s")` .............(4)
Where a is some positive constant. From equation (3) and (4)
− a (T − Ts) = `"ms" "dT"/"dt"`
`"dT"/("T" - "T"_"s") = -"a"/"ms" "dt"` .......(5)
Integrating equation (5) on both sides,
`int "dT"/("T" - "T"_"s") = - int "a"/"ms" "dt"`
ln (T − Ts) = `"a"/"ms" "t" + "b"_1`
Where b1, is the constant of integration. Taking exponential both sides, we get
T = `"T"_"s" + "b"_2"e"^(-"a"/"ms""t")` ........(6)
here b2 = `"e"^("b"_1)` = constant
APPEARS IN
संबंधित प्रश्न
Choose the correct option.
If two temperatures differ by 25° C on Celsius scale, the difference in temperature on Fahrenheit scale is
Obtain an ideal gas law from Boyle’s and Charles’ law.
Give the expression for linear thermal expansion.
Define latent heat capacity.
Write the unit of latent heat capacity.
Define thermal conductivity.
Discuss the ideal gas laws.
Discuss various modes of heat transfer.
Calculate the number of moles of air is in the inflated balloon at room temperature as shown in the figure.

The radius of the balloon is 10 cm, and the pressure inside the balloon is 180 kPa.
The temperature of a uniform rod of length L having a coefficient of linear expansion αL is changed by ∆T. Calculate the new moment of inertia of the uniform rod about the axis passing through its center and perpendicular to an axis of the rod.
