Advertisements
Advertisements
Question
Explain in detail Newton’s law of cooling.
Solution
Newton’s law of cooling: Newton’s law of cooling states that the rate of loss of heat of a body is directly proportional to the difference in the temperature between that body and its surroundings.
`"dQ"/"dt" ∝ ("T" - "T"_"s")` ............(1)
The negative sign indicates that the quantity of heat lost by liquid goes on decreasing with time. Where,
T = Temperature of the object
Ts = Temperature of the surrounding
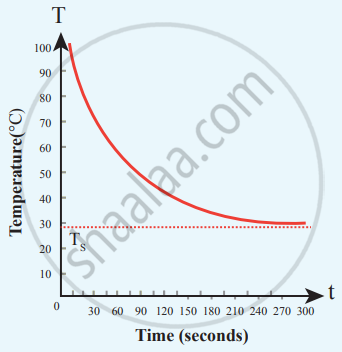
Cooling of hot water with time
From the graph in the figure, it is clear that the rate of cooling is high initially and decreases with falling temperature.
Let us consider an object of mass m and specific heat capacity s at temperature T. Let Ts be the temperature of the surroundings. If the temperature falls by a small amount dT in time dt, then the amount of heat lost is,
dQ = msdT .........(2)
Dividing both sides of equation (2) by dt
`"dQ"/"dt" = "msd"/"dt"` .........(3)
From Newton’s law of cooling `"dQ"/"dt" ∝ ("T" - "T"_"s")`
`"dQ"/"dt" = - "a"("T" - "T"_"s")` .............(4)
Where a is some positive constant. From equation (3) and (4)
− a (T − Ts) = `"ms" "dT"/"dt"`
`"dT"/("T" - "T"_"s") = -"a"/"ms" "dt"` .......(5)
Integrating equation (5) on both sides,
`int "dT"/("T" - "T"_"s") = - int "a"/"ms" "dt"`
ln (T − Ts) = `"a"/"ms" "t" + "b"_1`
Where b1, is the constant of integration. Taking exponential both sides, we get
T = `"T"_"s" + "b"_2"e"^(-"a"/"ms""t")` ........(6)
here b2 = `"e"^("b"_1)` = constant
APPEARS IN
RELATED QUESTIONS
Choose the correct option.
If two temperatures differ by 25° C on Celsius scale, the difference in temperature on Fahrenheit scale is
Define molar specific heat capacity.
Give the expression for volume thermal expansion.
Define latent heat capacity.
Write the unit of latent heat capacity.
Discuss the ideal gas laws.
Explain Calorimetry and derive an expression for final temperature when two thermodynamic systems are mixed.
Discuss various modes of heat transfer.
A man starts bicycling in the morning at a temperature around 25°C, he checked the pressure of tire which is equal to be 500 kPa. Afternoon he found that the absolute pressure in the tyre is increased to 520 kPa. By assuming the expansion of tyre is negligible, what is the temperature of tyre at afternoon?
Another name for thermal energy is ______
