Advertisements
Advertisements
प्रश्न
Explain the Total expenditure method and Geometric method of measuring price elasticity of demand.
Write a short note:
Geometric method of measuring price elasticity of demand.
Answer the details:
Explain the Ratio method and Geometric method of measuring Elasticity of Demand.
उत्तर
- Total Expenditure Method: This method was developed by Prof. Marshall. In this method, the total amount of expenditure before and after the price change is compared.
Here the total expenditure refers to the product of price and quantity demanded.
Total expenditure = Price × Quantity demanded
In this connection, Marshall has given the following propositions:
A) Relatively elastic demand (Ed >1): When with a given change in the price of a commodity, total outlay increases, the elasticity of demand is greater than one.
B) Unitary elastic demand (Ed = 1): When the price falls or rises, total outlay does not change or remains constant, the elasticity of demand is equal to one.
C) Relatively inelastic demand (Ed < 1): When with a given change in the price of a commodity, total outlay decreases, and the elasticity of demand is less than one. - Geometric Method: Prof. Marshall has developed another method to measure the elasticity of demand, which is known as the point method or geometric method. The ratio method and total outlay methods are unable to measure the elasticity of demand at a given point on the demand curve.
At any point on the demand curve, the elasticity of demand is measured with the help of the following formula:
`"Point elasticity of demand (Ed)" = "Lower segment of demand curve below a given point (L)"/"Upper segment of demand curve above a given point (U)"`
The demand curve may be either linear or non-linear as shown below:
A) Linear Demand Curve: When the demand curve is linear i.e. a straight line, we extend the demand curve to meet the Y axis at ‘A’ and X axis at ‘B’. Price elasticity of demand at ‘X’ axis is zero and ‘Y’ axis is infinite. The elasticity of demand will be different at each point.
Let us assume that AB is a demand curve and its length is 8 cm. Point elasticity at various points on a linear demand curve can be measured as follows:
1) At point P, the point elasticity is measured as:
P = `"PB"/"PA" = 4/4 = 1`
Thus, at point P, demand is unitary elastic (ed = 1).
2) At point P1, the point elasticity is measured as:
P1 = `("P"_1"B")/("P"_1"A") = 2/6 = 0.33`
Thus, at point P1, demand is relatively inelastic (ed < 1).
3) At point P2, the point elasticity is measured as:
`"P"_2 = ("P"_2"B")/("P"_2"A") = 6/2 = 3`
Thus, at point P2, demand is relatively elastic (ed > 1).
4) At point A, the point elasticity is ∞ (perfectly elastic demand).
5) At point B, the point elasticity is zero (perfectly inelastic demand.)
B) Non-linear demand curve: When the demand curve is non-linear i.e. convex to origin, to measure the price elasticity of demand, we have to draw a tangent ‘AB’ touching the given point on the demand curve and extend it to meet ‘Y’ axis at point ‘A’ and ‘X’ axis at point ‘B’.
Ed = `"Lower segment of the tangent below a given point"/"Upper segment of the tangent above a given point" = "L"/"U"`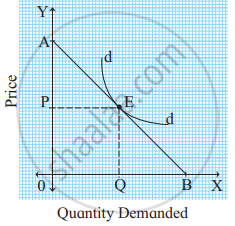
If EB = EA (Ed = 1) - Unitary elastic demand
EB > EA (Ed > 1) - Relatively elastic demand
EB < EA (Ed < 1) - Relatively inelastic demand - Ratio or Percentage method: The ratio method was developed by Prof. Marshall. According to this method, the elasticity of demand is measured by dividing the percentage change in demand by the percentage change in price. The percentage method is also known as the Arithmetic method. Price elasticity is measured as:
Ed = `"Percentage change in Quantity demanded"/"Percentage change in Price"`
Ed = `(%Delta"Q")/(%Delta"P")`
Mathematically, the above formula can be presented as under.
Ed = `(Delta"Q")/"Q" ÷ (Delta"P")/"P"`
∴ Ed = `(Delta"Q")/"Q" xx "P"/(Delta"P")`
Q = Original quantity demanded
ΔQ = Difference between the new quantity and original quantity demanded.
P = Original price
ΔP = Difference between the new price and original price
APPEARS IN
संबंधित प्रश्न
The price elasticity of demand on a linear demand curve at the X-axis is ______.
Complete the correlation:
Straight-line demand curve : Linear demand curve :: _______ : non-linear demand curve.
Explain the total outlay method of measuring elasticity of demand?
Explain the Ratio method of measuring price elasticity of demand.
Explain the Ratio or percentage method of measuring price elasticity of demand.
Complete the correlation:
Ratio method : `"Ed"= (%\Delta"Q")/(%\Delta"P") :: "______" : "Ed" = "Lower segment"/("Upper segment"`
Complete the correlation.
Ratio method : Ed = `(% Delta "Q")/(%Delta"P"):: "______" : Ed = ("Lower segment")/("Upper segment")`
Complete the correlation :
Ratio method : Ed = `(%Delta"Q")/(%Delta"P")` :: ______ : Ed = `"Lower segment"/"Upper segment"`
Complete the correlation:
Ratio method: Ed = `(%\Delta"Q")/(%\Delta"P")`:: ______ : Ed = `("Lower segment")/("Upper segment")`
Complete the correlation:
______ : Straight line demand curve : : Non-linear demand curve : Curved line demand curve
Complete the correlation:
Ratio method : Ed = `(%Δ Q) / (% Δ P)` :: ______ : Ed = `("Lower segment")/("Upper segment")`
Complete the correlation:
Ratio method : Ed = `(%DeltaQ)/(%DeltaP)` :: ______ : Ed : `"Lower segment"/"Upper segment"`
Complete the correlation :
Ratio method : Ed = `(%ΔQ)/(%ΔP)` :: _____ : Ed = `"Lower segment"/"Upper segment"`
Complete the correlation:
Ratio method : Ed = `(%ΔQ)/(%ΔP)` : : ______ : Ed = `("Lower segment")/("Upper segment")`
Complete the correlation:
Ratio method : Ed = `("%"\Delta"Q")/("%"\Delta"P")` :: ______ : Ed =`("Lower segment") /("Upper segment")`
Complete the correlation:
Ratio method : Ed = `\(%Delta "Q") /(%\Delta "P"` :: ______ : Ed = `\("Lower segment")/("Upper segment")`
Ratio method : Ed = `(%DeltaQ)/(%DeltaP)` :: ______ : Ed = `("Lower segment")/("Upper segment")`
If demand increases by 50% due to an increase in price by 75%, calculate the price elasticity of demand.
As a result of a 5% increase in price, the demand for commodity X increases by 12%. The price elasticity of demand will be ______.
If the percentage increase in the quantity of a commodity is smaller than the percentage fall in its price, the coefficient of price elasticity of demand is ______.
Assertion (A): Suppose that a 2 per cent drop in the price of chocolate causes a 2 per cent increase in quantity demanded. This case is termed unit elasticity.
Reason (R): In this example, Ed is exactly 1 (or unity). Ed = `2/2=1`
Select the commodities from the following which have inelastic demand:
Is the demand for the following commodities elastic or inelastic?
- Salt
- Foodgrains
- Petrol
- Needles
- Green vegetables
- Four Square cigarettes
- Water
When the price of a commodity falls by 80%, the quantity demanded increases by 100%. Find out its price elasticity of demand.
Ed = `100/80 = 1.25`
State the formula for calculating the price elasticity of demand using the percentage method.
The price of a commodity falls from ₹15 to ₹10. As a result, demand rises from 100 units to 150 units, Use the expenditure method to find the price elasticity of demand.
Study the table given below and state whether demand is elastic or inelastic. Give reasons for your answer.
| Price in (₹) | Total outlay (₹) |
| 5 | 25 |
| 3 | 18 |
The price of milk rises from ₹ 26.00 to ₹ 30.00 per litre and its demand falls from four litres per day to two litres per day. Calculate the elasticity demand for milk.
With the help of a diagram, explain the condition when EP > 1.
With the help of a diagram, explain the condition when EP < 1.
With the help of a diagram, explain the condition when Ep = 1.
Give two examples of inelastic demand.
What is meant by unitary elastic demand?
Give two examples of unitary elastic demand.
Arrange the following coefficients of price elasticity of demand in ascending order.
−0.87, −0.53, −31 , −0.80
State whether demand for the following goods is elastic or inelastic?
- car
- textbooks
- cigarettes
- diamonds
- milk
- seasonal vegetables
- coal
- Dawat basmati rice
- needles
- colour T.V.
From the following state whether the price elasticity of demand is inelastic, relatively elastic, highly elastic or highly inelastic. Give reasons to support your answer.
demand for school uniform
From the following state whether the price elasticity of demand is inelastic, relatively elastic, highly elastic or highly inelastic. Give reasons to support your answer.
demand for refrigerators
From the following state whether the price elasticity of demand is inelastic, relatively elastic, highly elastic or highly inelastic. Give reasons to support your answer.
demand for electricity
From the following state whether the price elasticity of demand is inelastic, relatively elastic, highly elastic or highly inelastic. Give reasons to support your answer.
demand for personal computers
From the following state whether the price elasticity of demand is inelastic, relatively elastic, highly elastic or highly inelastic. Give reasons to support your answer.
Demand for precious stones and costly jewellery
Ratio method : Ed = `(%ΔQ) /(%ΔP)` ______ :: Ed = `("Lower segment")/("Upper segment")`
