Advertisements
Advertisements
प्रश्न
Express the number as a product of its prime factor:
156
उत्तर
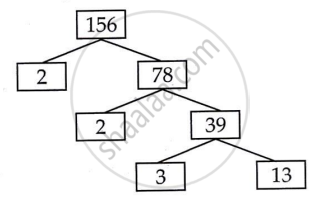
∴ 156 = 2 × 2 × 3 × 13
= 22 × 3 × 13
APPEARS IN
संबंधित प्रश्न
Consider the number 6n where n is a natural number. Check whether there is any value of n ∈ N for which 6n is divisible by 7.
Find the LCM and HCF of the following integers by applying the prime factorisation method.
12, 15 and 21
Given that HCF (306, 657) = 9, find LCM (306, 657).
A merchant has 120 liters of oil of one kind, 180 liters of another kind and 240 liters of third kind. He wants to sell the oil by filling the three kinds of oil in tins of equal capacity. What should be the greatest capacity of such a tin?
Find the LCM and HCF of the following integers by applying the prime factorisation method:
24, 15 and 36
Can two numbers have 16 as their HCF and 380 as their LCM? Give reason.
Write the exponent of 2 in the price factorization of 144.
If the prime factorization of a natural number n is 23 ✕ 32 ✕ 52 ✕ 7, write the number of consecutive zeros in n.
Find the LCM and HCF of the following integers by applying the prime factorisation method.
17, 23 and 29
What is the smallest number that when divided by three numbers such as 35, 56 and 91 leaves remainder 7 in each case?
Find the least number that is divisible by the first ten natural numbers
The sum of the exponents of the prime factors in the prime factorization of 1729 is
If two positive integers A and B can be expressed as A = xy3 and B = x4y2z; x, y being prime numbers then HCF (A, B) is ______.
The largest number which divides 60 and 75, leaving remainders 8 and 10 respectively, is ______.
n2 – 1 is divisible by 8, if n is ______.
If two positive integers a and b are written as a = x3 y2 and b = xy3; x, y are prime numbers, then HCF (a, b) is ______.
Find the HCF and LCM of 72 and 120.
The prime factorisation of the number 2304 is ______.
The mean of first ten natural numbers is ______.
