Advertisements
Advertisements
प्रश्न
Express the number as a product of its prime factor:
156
उत्तर
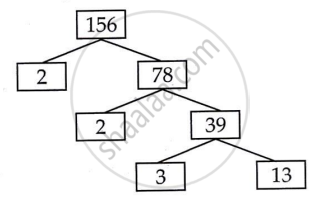
∴ 156 = 2 × 2 × 3 × 13
= 22 × 3 × 13
APPEARS IN
संबंधित प्रश्न
Express the number as a product of its prime factor:
140
State fundamental theorem of arithmetic?
Find the LCM and HCF of the following pair of integers and verify that LCM × HCF = Product of the two numbers.
26 and 91
Find the LCM and HCF of the following integers by applying the prime factorisation method:
24, 15 and 36
Can two numbers have 16 as their HCF and 380 as their LCM? Give reason.
The HCF of two numbers is 145 and their LCM is 2175. If one number is 725, find the other.
Write the exponent of 2 in the price factorization of 144.
If the prime factorization of a natural number n is 23 ✕ 32 ✕ 52 ✕ 7, write the number of consecutive zeros in n.
Express the number as a product of its prime factor:
5005
Find the LCM and HCF of the following pair of integers and verify that LCM × HCF = product of the two numbers.
336 and 54
If m, n are natural numbers, for what values of m, does 2n × 5m ends in 5?
Find the H.C.F. of 252525 and 363636
If two positive integers A and B can be expressed as A = xy3 and B = x4y2z; x, y being prime numbers then HCF (A, B) is ______.
According to the fundamental theorem of arithmetic, if T (a prime number) divides b2, b > 0, then ______.
For some integer q, every odd integer is of the form ______.
If two positive integers a and b are written as a = x3 y2 and b = xy3; x, y are prime numbers, then HCF (a, b) is ______.
Let a and b be two positive integers such that a = p3q4 and b = p2q3, where p and q are prime numbers. If HCF (a, b) = pmqn and LCM (a, b) = prqs, then (m + n)(r + s) = ______.
If HCF (72, 120) = 24, then LCM (72, 120) is ______.
National Art convention got registrations from students from all parts of the country, of which 60 are interested in music, 84 are interested in dance and 108 students are interested in handicrafts. For optimum cultural exchange, organisers wish to keep them in minimum number of groups such that each group consists of students interested in the same artform and the number of students in each group is the same. Find the number of students in each group. Find the number of groups in each art form. How many rooms are required if each group will be allotted a room?
