Advertisements
Advertisements
प्रश्न
Find the LCM and HCF of the following pair of integers and verify that LCM × HCF = product of the two numbers.
336 and 54
उत्तर
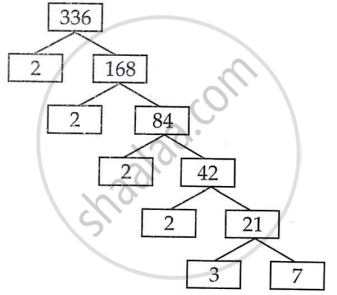 |
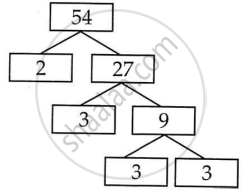 |
336 = 2 × 2 × 2 × 2 × 3 × 7
54 = 2 × 3 × 3 × 3
L.C.M of 336 and 54 = 2 × 3 × 3 × 3
L.C.M of 336 and 54 = 3024
H.C.F of 336 and 54 = 6
We know that,
L.C.M × H.C.F = First Numbers × Second Number
3024 × 6 = 336 × 26
18144 = 18144
Thus, LCM × HCF = Product of two numbers.
संबंधित प्रश्न
Express the number as a product of its prime factor:
140
State fundamental theorem of arithmetic?
Determine the prime factorisation of each of the following positive integer:
58500
Find the LCM and HCF of the following pair of integers and verify that LCM × HCF = Product of the two numbers.
26 and 91
Write down the decimal expansions of the following rational numbers by writing their denominators in the form 2m × 5n, where, m, n are non-negative integers. \[\frac{3}{8}\]
Find the least positive value of x such that 89 ≡ (x + 3) (mod 4)
Three farmers have 490 kg, 588 kg and 882 kg of wheat respectively. Find the maximum capacity of a bag so that the wheat can be packed in exact number of bags.
For some integer p, every odd integer is of the form ______.
If two positive integers A and B can be expressed as A = xy3 and B = x4y2z; x, y being prime numbers then HCF (A, B) is ______.
If LCM(x, 18) = 36 and HCF(x, 18) = 2, then x is ______.
If the HCF of 65 and 117 is expressible in the form 65m – 117, then the value of m is ______.
If two positive integers p and q can be expressed as p = ab2 and q = a3b; a, b being prime numbers, then LCM (p, q) is ______.
The least number that is divisible by all the numbers from 1 to 10 (both inclusive) is ______.
Find the HCF and LCM of 26, 65 and 117, using prime factorisation.
If HCF (72, 120) = 24, then LCM (72, 120) is ______.
The HCF of the smallest 2-digit number and the smallest composite number is ______.
The prime factorisation of the number 5488 is ______.
Three bells toll at intervals of 9, 12 and 15 minutes respectively. If they start tolling together, after what time will they next toll together?
