Advertisements
Advertisements
प्रश्न
Find the LCM and HCF of the following integers by applying the prime factorisation method.
12, 15 and 21
उत्तर
 |
 |
 |
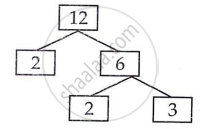
12 = 2 × 2 × 3
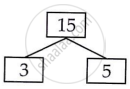
15 = 3 × 5
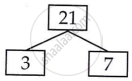
21 = 3 × 7
H.C.F of 12, 15 and 21 = 3
L.CM of 12, 15 and 21 = 2 × 2 × 3 × 5 × 7
L.C.M of 12, 15 and 21 = 420
संबंधित प्रश्न
Consider the number 12n where n is a natural number. Check whether there is any value of n ∈ N for which 12n ends with the digital zero.
Find HCF and LCM of 404 and 96 and verify that HCF × LCM = Product of the two given numbers.
State fundamental theorem of arithmetic?
Write the exponent of 2 in the price factorization of 144.
Write the sum of the exponents of prime factors in the prime factorization of 98.
Express the number as a product of its prime factor:
3825
Find the LCM and HCF of the following pair of integers and verify that LCM × HCF = product of the two numbers.
336 and 54
Find the L.C.M. and H.C.F. of 408 and 170 by applying the fundamental theorem of Arithmetic
What is the smallest number that when divided by three numbers such as 35, 56 and 91 leaves remainder 7 in each case?
If two positive integers A and B can be expressed as A = xy3 and B = x4y2z; x, y being prime numbers then HCF (A, B) is ______.
The product of two consecutive natural numbers is always ______.
According to the fundamental theorem of arithmetic, if T (a prime number) divides b2, b > 0, then ______.
If LCM(x, 18) = 36 and HCF(x, 18) = 2, then x is ______.
The largest number which divides 70 and 125, leaving remainders 5 and 8, respectively, is ______.
Can two numbers have 18 as their HCF and 380 as their LCM? Give reasons.
Find the HCF and LCM of 26, 65 and 117, using prime factorisation.
The HCF of the smallest 2-digit number and the smallest composite number is ______.
The prime factorisation of the number 5488 is ______.
National Art convention got registrations from students from all parts of the country, of which 60 are interested in music, 84 are interested in dance and 108 students are interested in handicrafts. For optimum cultural exchange, organisers wish to keep them in minimum number of groups such that each group consists of students interested in the same artform and the number of students in each group is the same. Find the number of students in each group. Find the number of groups in each art form. How many rooms are required if each group will be allotted a room?
