Advertisements
Advertisements
Question
Find the LCM and HCF of the following integers by applying the prime factorisation method.
12, 15 and 21
Solution
 |
 |
 |
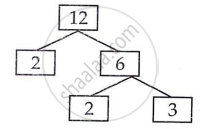
12 = 2 × 2 × 3
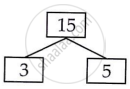
15 = 3 × 5
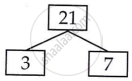
21 = 3 × 7
H.C.F of 12, 15 and 21 = 3
L.CM of 12, 15 and 21 = 2 × 2 × 3 × 5 × 7
L.C.M of 12, 15 and 21 = 420
APPEARS IN
RELATED QUESTIONS
Consider the number 12n where n is a natural number. Check whether there is any value of n ∈ N for which 12n ends with the digital zero.
What is the HCF of the smallest prime number and the smallest composite number?
State Fundamental Theorem of Arithmetic.
Express the number as a product of its prime factor:
156
Express the number as a product of its prime factor:
5005
Find the H.C.F. of 252525 and 363636
If p1x1 × p2x2 × p3x3 × p4x4 = 113400 where p1, p2, p3, p4 are primes in ascending order and x1, x2, x3, x4, are integers, find the value of p1, p2, p3, p4 and x1, x2, x3, x4
Find the least positive value of x such that 89 ≡ (x + 3) (mod 4)
Express 98 as a product of its primes.
Three farmers have 490 kg, 588 kg and 882 kg of wheat respectively. Find the maximum capacity of a bag so that the wheat can be packed in exact number of bags.
If two positive integers A and B can be expressed as A = xy3 and B = x4y2z; x, y being prime numbers then HCF (A, B) is ______.
When a number is divided by 7, its remainder is always ______.
If the HCF of 65 and 117 is expressible in the form 65m – 117, then the value of m is ______.
Explain why 3 × 5 × 7 + 7 is a composite number.
On a morning walk, three persons step off together and their steps measure 40 cm, 42 cm and 45 cm, respectively. What is the minimum distance each should walk so that each can cover the same distance in complete steps?
Let a and b be two positive integers such that a = p3q4 and b = p2q3, where p and q are prime numbers. If HCF (a, b) = pmqn and LCM (a, b) = prqs, then (m + n)(r + s) = ______.
Find the HCF and LCM of 26, 65 and 117, using prime factorisation.
(HCF × LCM) for the numbers 70 and 40 is ______.
If HCF (72, 120) = 24, then LCM (72, 120) is ______.
If two positive integers a and b are written as a = x3y2 and b = xy3, where x, y are prime numbers, then the result obtained by dividing the product of the positive integers by the LCM (a, b) is ______.
