Advertisements
Advertisements
Question
Find the LCM and HCF of the following pair of integers and verify that LCM × HCF = product of the two numbers.
336 and 54
Solution
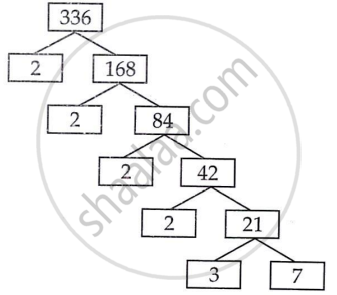 |
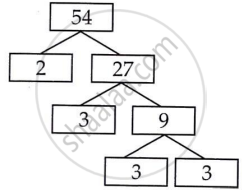 |
336 = 2 × 2 × 2 × 2 × 3 × 7
54 = 2 × 3 × 3 × 3
L.C.M of 336 and 54 = 2 × 3 × 3 × 3
L.C.M of 336 and 54 = 3024
H.C.F of 336 and 54 = 6
We know that,
L.C.M × H.C.F = First Numbers × Second Number
3024 × 6 = 336 × 26
18144 = 18144
Thus, LCM × HCF = Product of two numbers.
APPEARS IN
RELATED QUESTIONS
Check whether 6n can end with the digit 0 for any natural number n.
Determine the prime factorisation of each of the following positive integer:
20570
Can two numbers have 16 as their HCF and 380 as their LCM? Give reason.
Write down the decimal expansions of the following rational numbers by writing their denominators in the form 2m × 5n, where, m, n are non-negative integers. \[\frac{3}{8}\]
Write the sum of the exponents of prime factors in the prime factorization of 98.
If the product of two numbers is 1080 and their HCF is 30, find their LCM.
Express the number as a product of its prime factor:
7429
Find the LCM and HCF of the following integers by applying the prime factorisation method.
8, 9 and 25
For what value of natural number n, 4n can end with the digit 6?
Find the L.C.M. and H.C.F. of 408 and 170 by applying the fundamental theorem of Arithmetic
Find the greatest number consisting of 6 digits which is exactly divisible by 24, 15, 36?
Find the least number that is divisible by the first ten natural numbers
Find the least positive value of x such that 89 ≡ (x + 3) (mod 4)
The number in the form of 4p + 3, where p is a whole number, will always be ______.
When a number is divided by 7, its remainder is always ______.
If LCM(x, 18) = 36 and HCF(x, 18) = 2, then x is ______.
The largest number which divides 70 and 125, leaving remainders 5 and 8, respectively, is ______.
The least number that is divisible by all the numbers from 1 to 10 (both inclusive) is ______.
Assertion (A): The HCF of two numbers is 5 and their product is 150. Then their LCM is 40.
Reason(R): For any two positive integers a and b, HCF (a, b) × LCM (a, b) = a × b.
If two positive integers a and b are written as a = x3y2 and b = xy3, where x, y are prime numbers, then the result obtained by dividing the product of the positive integers by the LCM (a, b) is ______.
