Advertisements
Advertisements
Question
Find the greatest number consisting of 6 digits which is exactly divisible by 24, 15, 36?
Solution
To find L.C.M. of 24, 15, 36
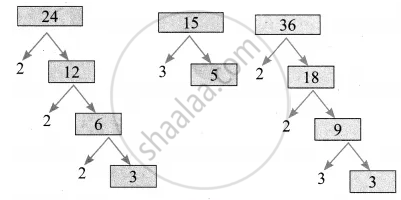
24 = 23 × 3
15 = 3 × 5
36 = 22 × 32
| Prime factors of 24, 15, 36 |
Greatest Exponents |
| 2 | 3 |
| 3 | 2 |
| 5 | 1 |
∴ L.C.M. = 23 × 32 × 51
= 8 × 9 × 5
= 360
If a number has to be exactly divisible by 24, 15, and 36, then it has to be divisible by 360. Greatest 6 digit number is 999999.
Common multiplies of 24, 15, 36 with 6 digits are 103680, 116640, 115520, …, 933120, 999720 with six digits.
∴ The greatest number consisting of 6 digits which is exactly divisible by 24, 15, 36 is 999720.
APPEARS IN
RELATED QUESTIONS
State fundamental theorem of arithmetic?
Determine the prime factorisation of each of the following positive integer:
20570
Find the LCM and HCF of the following pair of integers and verify that LCM × HCF = Product of the two numbers.
26 and 91
Write down the decimal expansions of the following rational numbers by writing their denominators in the form 2m × 5n, where, m, n are non-negative integers.\[\frac{13}{125}\]
Write the sum of the exponents of prime factors in the prime factorization of 98.
If LCM(x, 18) = 36 and HCF(x, 18) = 2, then x is ______.
On a morning walk, three persons step off together and their steps measure 40 cm, 42 cm and 45 cm, respectively. What is the minimum distance each should walk so that each can cover the same distance in complete steps?
Find the HCF and LCM of 72 and 120.
Two numbers are in the ratio 2 : 3 and their LCM is 180. What is the HCF of these numbers?
The prime factorisation of the number 5488 is ______.
