Advertisements
Advertisements
Question
Find the LCM and HCF of the following pair of integers and verify that LCM × HCF = Product of the two numbers.
26 and 91
Solution
 |
|
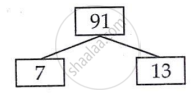
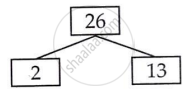
26 = 2 × 13
91 = 7 × 13
L.C.M of 26 and 91 = 2 × 7 × 13
L.C.M of 26 and 91 = 182
H.C.F of 26 and 91 = 13
We know that,
Now, LCM × HCF = First number × Second number
⇒ 182 × 13 = 26 × 91
⇒ 2366 = 2366
i.e., LCM × HCF = Product of two numbers.
APPEARS IN
RELATED QUESTIONS
Consider the number 12n where n is a natural number. Check whether there is any value of n ∈ N for which 12n ends with the digital zero.
Express the number as a product of its prime factor:
140
Given that HCF (306, 657) = 9, find LCM (306, 657).
Determine the prime factorisation of each of the following positive integer:
58500
Determine the prime factorisation of each of the following positive integer:
45470971
Find the LCM and HCF of the following integers by applying the prime factorisation method:
24, 15 and 36
What is the smallest number that when divided by three numbers such as 35, 56 and 91 leaves remainder 7 in each case?
The product of two consecutive natural numbers is always ______.
The number in the form of 4p + 3, where p is a whole number, will always be ______.
When a number is divided by 7, its remainder is always ______.
The ratio of LCM and HCF of the least composite and the least prime numbers is ______.
The largest number which divides 70 and 125, leaving remainders 5 and 8, respectively, is ______.
If two positive integers p and q can be expressed as p = ab2 and q = a3b; a, b being prime numbers, then LCM (p, q) is ______.
Show that 12n cannot end with the digit 0 or 5 for any natural number n.
Show the 6n cannot end with digit 0 for any natural number 'n'.
Find the HCF and LCM of 26, 65 and 117, using prime factorisation.
Assertion (A): The HCF of two numbers is 5 and their product is 150. Then their LCM is 40.
Reason(R): For any two positive integers a and b, HCF (a, b) × LCM (a, b) = a × b.
If n is a natural number, then 8n cannot end with digit