Advertisements
Advertisements
प्रश्न
Find the LCM and HCF of the following pair of integers and verify that LCM × HCF = Product of the two numbers.
26 and 91
उत्तर
 |
|
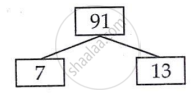
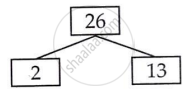
26 = 2 × 13
91 = 7 × 13
L.C.M of 26 and 91 = 2 × 7 × 13
L.C.M of 26 and 91 = 182
H.C.F of 26 and 91 = 13
We know that,
Now, LCM × HCF = First number × Second number
⇒ 182 × 13 = 26 × 91
⇒ 2366 = 2366
i.e., LCM × HCF = Product of two numbers.
APPEARS IN
संबंधित प्रश्न
Consider the number 12n where n is a natural number. Check whether there is any value of n ∈ N for which 12n ends with the digital zero.
Express the number as a product of its prime factor:
140
Given that HCF (306, 657) = 9, find LCM (306, 657).
Find the LCM and HCF of the following integers by applying the prime factorisation method:
24, 15 and 36
Write the sum of the exponents of prime factors in the prime factorization of 98.
Express the number as a product of its prime factor:
5005
Find the LCM and HCF of the following integers by applying the prime factorisation method.
17, 23 and 29
Find the LCM and HCF of the following integers by applying the prime factorisation method.
8, 9 and 25
If 13824 = 2a × 3b then find a and b
If two positive integers A and B can be expressed as A = xy3 and B = xiy2z; x, y being prime numbers, the LCM (A, B) is ______.
If two positive integers A and B can be expressed as A = xy3 and B = x4y2z; x, y being prime numbers then HCF (A, B) is ______.
The product of two consecutive natural numbers is always ______.
When a number is divided by 7, its remainder is always ______.
The largest number which divides 70 and 125, leaving remainders 5 and 8, respectively, is ______.
Can two numbers have 18 as their HCF and 380 as their LCM? Give reasons.
Show that 12n cannot end with the digit 0 or 5 for any natural number n.
The prime factorisation of the number 2304 is ______.
If n is a natural number, then 8n cannot end with digit