Advertisements
Advertisements
प्रश्न
Find the LCM and HCF of the following pair of integers and verify that LCM × HCF = product of the two numbers.
510 and 92
उत्तर
 |
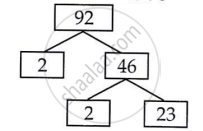 |
510 = 2 × 3 × 5 × 17
92 = 2 × 2 × 23
Therefore, 510 = 2 × 3 × 5 × 17 ...(A)
92 = 2 × 46
= 2 × 2 × 23 ...(B)
From (A) and (B) HCF of 510 and 92 is = 2 and their
LCM is 2 × 2 × 3 × 5 × 17 × 23 = 23460
Product of the LCM and HCF = 2 × 23460 = 46920
Product of the two numbers = 510 × 92 = 46920
Therefore, it is proved that LCM × HCF = Product of the two numbers.
संबंधित प्रश्न
Consider the number 6n where n is a natural number. Check whether there is any value of n ∈ N for which 6n is divisible by 7.
Explain why 7 × 11 × 13 + 13 and 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 are composite numbers.
What is the HCF of the smallest prime number and the smallest composite number?
Determine the prime factorisation of each of the following positive integer:
20570
Determine the prime factorisation of each of the following positive integer:
45470971
Find the LCM and HCF of the following pair of integers and verify that LCM × HCF = Product of the two numbers.
26 and 91
Find the LCM and HCF of the following integers by applying the prime factorisation method:
24, 15 and 36
The HCF of two numbers is 145 and their LCM is 2175. If one number is 725, find the other.
Express the number as a product of its prime factor:
5005
Express the number as a product of its prime factor:
7429
If p1x1 × p2x2 × p3x3 × p4x4 = 113400 where p1, p2, p3, p4 are primes in ascending order and x1, x2, x3, x4, are integers, find the value of p1, p2, p3, p4 and x1, x2, x3, x4
Find the least positive value of x such that 89 ≡ (x + 3) (mod 4)
For some integer p, every odd integer is of the form ______.
The largest number which divides 70 and 125, leaving remainders 5 and 8, respectively, is ______.
If two positive integers p and q can be expressed as p = ab2 and q = a3b; a, b being prime numbers, then LCM (p, q) is ______.
Show that 12n cannot end with the digit 0 or 5 for any natural number n.
Read the following passage:
|
Khushi wants to organize her birthday party. Being health conscious, she decided to serve only fruits in her birthday party. She bought 39 apples and 60 bananas and decided to distribute fruits equally among all. |
Based on the above information, answer the following questions:
- How many guests Khushi can invite at the most?
- How many apples and bananas will each guest get?
-
- If Khushi decides to add 42 mangoes, how many guests Khushi can invite at the most?
OR - If the cost of 1 dozen of bananas is ₹ 60, the cost of 1 apple is ₹ 15 and cost of 1 mango is ₹ 20, find the total amount spent on 60 bananas, 36 apples and 42 mangoes.

- If Khushi decides to add 42 mangoes, how many guests Khushi can invite at the most?
The HCF of the smallest 2-digit number and the smallest composite number is ______.
The prime factorisation of the number 5488 is ______.
