Advertisements
Advertisements
प्रश्न
If 13824 = 2a × 3b then find a and b
उत्तर
If 13824 = 2a × 3b
Using the prime factorization tree
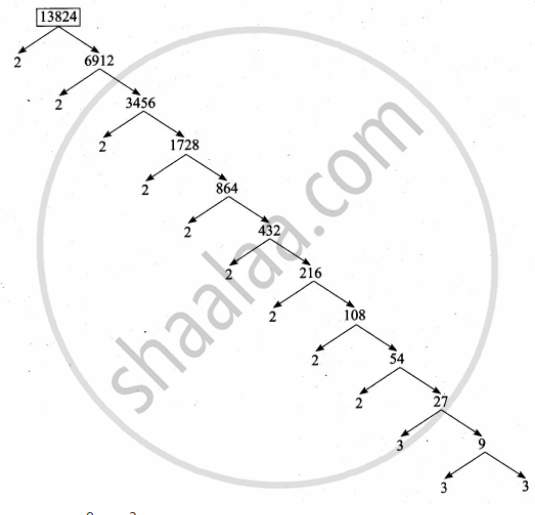
13824 = 29 × 33
Given 13824 = 2a × 3b
Compare we get a = 9 and b = 3
Aliter:
13824 = 29 × 33
Compare with
13824 = 2a × 3b
The value of a = 9 b = 3
APPEARS IN
संबंधित प्रश्न
Check whether 6n can end with the digit 0 for any natural number n.
State fundamental theorem of arithmetic?
Write down the decimal expansions of the following rational numbers by writing their denominators in the form 2m × 5n, where, m, n are non-negative integers.\[\frac{13}{125}\]
Express the number as a product of its prime factor:
156
The sum of the exponents of the prime factors in the prime factorization of 1729 is
The number in the form of 4p + 3, where p is a whole number, will always be ______.
n2 – 1 is divisible by 8, if n is ______.
Statement A (Assertion): If product of two numbers is 5780 and their HCF is 17, then their LCM is 340.
Statement R (Reason): HCF is always a factor of LCM.
Show the 6n cannot end with digit 0 for any natural number 'n'.
Three bells toll at intervals of 9, 12 and 15 minutes respectively. If they start tolling together, after what time will they next toll together?
