Advertisements
Advertisements
प्रश्न
Find the greatest number consisting of 6 digits which is exactly divisible by 24, 15, 36?
उत्तर
To find L.C.M. of 24, 15, 36
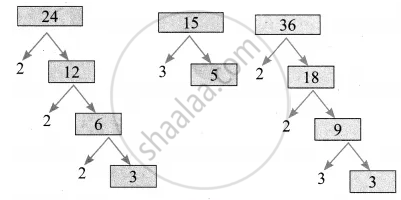
24 = 23 × 3
15 = 3 × 5
36 = 22 × 32
| Prime factors of 24, 15, 36 |
Greatest Exponents |
| 2 | 3 |
| 3 | 2 |
| 5 | 1 |
∴ L.C.M. = 23 × 32 × 51
= 8 × 9 × 5
= 360
If a number has to be exactly divisible by 24, 15, and 36, then it has to be divisible by 360. Greatest 6 digit number is 999999.
Common multiplies of 24, 15, 36 with 6 digits are 103680, 116640, 115520, …, 933120, 999720 with six digits.
∴ The greatest number consisting of 6 digits which is exactly divisible by 24, 15, 36 is 999720.
APPEARS IN
संबंधित प्रश्न
Find the LCM and HCF of the following integers by applying the prime factorisation method:
24, 15 and 36
Write the sum of the exponents of prime factors in the prime factorization of 98.
Express the number as a product of its prime factor:
7429
Find the L.C.M. and H.C.F. of 408 and 170 by applying the fundamental theorem of Arithmetic
LCM of the given number ‘x’ and ‘y’ where y is a multiple of ‘x’ is given by ______.
The ratio of LCM and HCF of the least composite and the least prime numbers is ______.
For some integer m, every even integer is of the form ______.
If two positive integers p and q can be expressed as p = ab2 and q = a3b; a, b being prime numbers, then LCM (p, q) is ______.
Show that 12n cannot end with the digit 0 or 5 for any natural number n.
The HCF of the smallest 2-digit number and the smallest composite number is ______.
