Advertisements
Advertisements
प्रश्न
Find the greatest number consisting of 6 digits which is exactly divisible by 24, 15, 36?
उत्तर
To find L.C.M. of 24, 15, 36
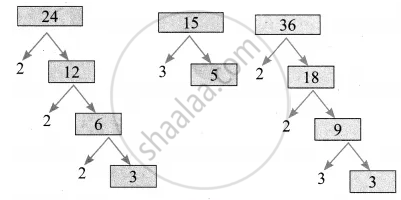
24 = 23 × 3
15 = 3 × 5
36 = 22 × 32
| Prime factors of 24, 15, 36 |
Greatest Exponents |
| 2 | 3 |
| 3 | 2 |
| 5 | 1 |
∴ L.C.M. = 23 × 32 × 51
= 8 × 9 × 5
= 360
If a number has to be exactly divisible by 24, 15, and 36, then it has to be divisible by 360. Greatest 6 digit number is 999999.
Common multiplies of 24, 15, 36 with 6 digits are 103680, 116640, 115520, …, 933120, 999720 with six digits.
∴ The greatest number consisting of 6 digits which is exactly divisible by 24, 15, 36 is 999720.
APPEARS IN
संबंधित प्रश्न
Find the LCM and HCF of the following integers by applying the prime factorisation method:
24, 15 and 36
Write the exponent of 2 in the price factorization of 144.
Write the sum of the exponents of prime factors in the prime factorization of 98.
Express the number as a product of its prime factor:
7429
There is a circular path around a sports field. Priya takes 18 minutes to drive one round of the field. Harish takes 12 minutes. Suppose they both start at the same point and at the same time and go in the same direction. After how many minutes will they meet?
If two positive integers A and B can be expressed as A = xy3 and B = x4y2z; x, y being prime numbers then HCF (A, B) is ______.
The largest number which divides 60 and 75, leaving remainders 8 and 10 respectively, is ______.
The number in the form of 4p + 3, where p is a whole number, will always be ______.
If n is a natural number, then 8n cannot end with digit
Three bells toll at intervals of 9, 12 and 15 minutes respectively. If they start tolling together, after what time will they next toll together?
