Advertisements
Advertisements
प्रश्न
Figure shows a small body of mass m placed over a larger mass M whose surface is horizontal near the smaller mass and gradually curves to become vertical. The smaller mass is pushed on the longer one at a speed v and the system is left to itself. Assume that all the surface are frictionless. (a) Find the speed of the larger block when the smaller block is sliding on the vertical part. (b) Find the speed of the smaller mass when it breaks off the larger mass at height h. (c) Find the maximum height (from the ground) that the smaller mass ascends. (d) Show that the smaller mass will again land on the bigger one. Find the distance traversed by the bigger block during the time when the smaller block was in its flight under gravity.

उत्तर
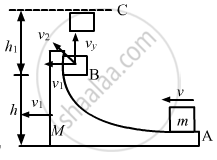
According to the question, mass m is given with a speed v over the larger mass M.
(a) When the smaller block travels on the vertical part, let the velocity of the bigger block be v1, towards left.
From the law of conservation of momentum (in the horizontal direction), we get:
\[mv = (M + m) v_1 \]
\[ \Rightarrow v_1 = \frac{mv}{M + m}\]
(b) When the smaller block breaks off, let its resultant velocity be v2.
Using the law a of conservation of energy, we get:
\[\left( \frac{1}{2} \right)m v^2 = \left( \frac{1}{2} \right)M v_1^2 + \left( \frac{1}{2} \right)m v_2^2 + mgh\]
\[ \Rightarrow {v_2}^2 = v^2 - \frac{M}{m} v_1^2 - 2gh . . . (i)\]
\[ \Rightarrow {v_2}^2 = v^2 \left[ 1 - \frac{M}{m} . \frac{m^2}{(M + m )^2} \right] - 2gh\]
\[ \Rightarrow v_2 = \left[ \frac{\left[ \left( m^2 + Mm + m^2 \right) \right] v^2}{(M + m )^2} - 2gh \right]^{1/2}\]
(c) Vertical component of the velocity v2 of mass m is given by,
\[{v_y}^2 = {v_2}^2 - {v_1}^2 \]
\[ = \frac{\left( M^2 + Mm + m^2 \right)}{\left( M + m \right)^2} v^2 - 2gh - \frac{m^2 v^2}{\left( M + m \right)^2}\]
\[ \left( \therefore v_1 = \frac{mv}{M + m} \right)\]
\[ \Rightarrow {v_y}^2 = \frac{M^2 + Mm + m^2 - m^2}{\left( M + m \right)^2} v^2 - 2gh\]
\[ \Rightarrow {v_y}^2 = \frac{M v^2}{\left( M + m \right)} - 2gh . . . (ii)\]
To determine the maximum height (from the ground),
Let us assume that the body rises to a height h1 over and above h.
\[\text{ Now }, \left( \frac{1}{2} \right)m v_y^2 = mg h_1 \]
\[ \Rightarrow h_1 = \frac{v_y^2}{2g} . . . (iii)\]
\[ \therefore \text{ Total height, H = h + h}_1 \]
\[ \Rightarrow H = h + \frac{v_y^2}{2g}\]
\[ \Rightarrow H = h+\frac{M v^2}{(M + m)2g}-h\]
\[\Rightarrow H = \frac{M v^2}{(M + m)2g}\]
(d) Because the smaller mass also has a horizontal component of velocity V1 at the time it breaks off from M (that has a velocity v1), the block m will again land on the block M.
The time of flight of block m after it breaks off is calculated as:
During the upward motion (BC),
\[0 = v_y - gt\]
\[ \Rightarrow t_1 = \frac{v_y}{g} = \frac{1}{g}\left[ \frac{M v^2}{(M + m)} - 2gh \right] . . . (4)\]
Thus, the time for which the smaller block is in flight is given by,
\[T = 2 t_1 \]
\[ = \frac{2}{g}\left[ \frac{M v^2 - 2(M + m)gh}{(M + m)} \right]\]
The distance travelled by the bigger block during this time is, \[S = v_1 T\]
APPEARS IN
संबंधित प्रश्न
Can the centre of mass of a body be at a point outside the body?
The weight Mg of an extended body is generally shown in a diagram to act through the centre of mass. Does it mean that the earth does not attract other particles?
All the particles of a body are situated at a distance R from the origin. The distance of the centre of mass of the body from the origin is
A body falling vertically downwards under gravity breaks in two parts of unequal masses. The centre of mass of the two parts taken together shifts horizontally towards
A body at rest breaks into two pieces of equal masses. The parts will move
A body has its centre of mass at the origin. the x-coordinates of the particles
(a) may be all positive
(b) may be all negative
(c) may be all non-negative
(d) may be positive for some cases and negative in other cases.
A body moving towards a finite body at rest collides with it. It is possible that
(a) both the bodies come to rest
(b) both the bodies move after collision
(c) the moving body comes to rest and the stationary body starts moving
(d) the stationary body remains stationary, the moving body changes its velocity.
In a head-on elastic collision of two bodies of equal masses
(a) the velocities are interchanged
(b) the speeds are interchanged
(c) the momenta are interchanged
(d) the faster body slows down and the slower body speeds up.
A block at rest explodes into three equal parts. Two parts start moving along X and Y axes respectively with equal speeds of 10 m/s. Find the initial velocity of the third part.
When tall building are constructed on earth, the duration of day-night slightly increases. Is it true?
A body of mass m makes an elastic collision with another identical body at rest. Show that if the collision is not head-on the bodies go at right angle to each other after the collision.
A small particle travelling with a velocity v collides elastically with a spherical body of equal mass and of radius r initially kept at rest. The centre of this spherical body is located a distance ρ(< r) away from the direction of motion of the particle (see figure below). Find the final velocities of the two particles.
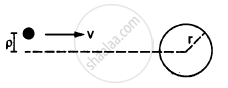
[Hint : The force acts along the normal to the sphere
through the contact. Treat the collision as onedimensional
for this direction. In the tangential direction no force acts and the velocities do not change].
