Advertisements
Advertisements
प्रश्न
Figure shows (vx, t) and (vy, t) diagrams for a body of unit mass. Find the force as a function of time.
 (a) |
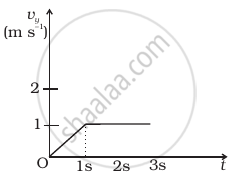 (b) |
उत्तर
In figure (a), we have vx = 2t for t < 1s and vx = 2(2 – t) for 1s < t < 2s
Hence the acceleration between 0s to 1s will be given by,
⇒ `a_x = (dv_x)/(dt) = (d^2t)/(dt) = 2 ms^-2`
Also `F_x = ma_x = 1 xx 2 = 2N` for t < 1s
And the acceleration between 1s to 2s will be given by,
⇒ `a_x = (dv_x)/(dt) = (2d(2 - t))/(dt) = - 2 ms^-2`
Also `F_x = ma_x = 1 xx (-2) = - 2N` for 1s < t < 2s
Now in figure (b), we have vy = t for t < 1s and vy = 1 for t > 1s
Hence the acceleration between 0s to 1s will be given by,
⇒ `a_y = (dv_y)/(dt) = (dt)/(dt) = 1 ms^-2`
Also `F_y = ma_y = 1 xx 1 = 1N` for t < 1s
And the acceleration between 1s to 3s will be given by,
⇒ `a_y = (dv_y)/(dt) = (d1)/(dt) = 0 ms^-2`
Also `F_y = ma_y = 1 xx 0 = 0N` for t > 1s
Now the resultant force will be given by,
⇒ `vecF = vec(F)_xhati + vec(F)_yhatj`
Hence,
⇒ `vecF = 2hati + hatj` for t < 1s
And,
⇒ `vecF = - 2hati` for 1s < t < 2s
And,
⇒ `vecF = 0` for t > 2s
APPEARS IN
संबंधित प्रश्न
Explain why it is easier to pull a lawn mower than to push it.
A mass m is suspended from a rigid support P by means of a massless string as shown in figure. A horizontal force F is applied at point O of the rope. The system is in equilibrium when the string makes an angle θ with the vertical. Then the relation between the tension T, force F and angle θ is P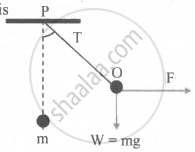
There are three forces F1, F2 and F3 acting on a body, all acting on a point P on the body. The body is found to move with uniform speed.
- Show that the forces are coplanar.
- Show that the torque acting on the body about any point due to these three forces is zero.
There are four forces acting at a point P produced by strings as shown in the figure, which is at rest. Find the forces F1 and F2.

