Question

When a body slides down from rest along a smooth inclined plane making an angle of 45° with the horizontal, it takes time T. When the same body slides down from rest along a rough inclined plane making the same angle and through the same distance, it is seen to take time pT, where p is some number greater than 1. Calculate the co-efficient of friction between the body and the rough plane.

Answer 1

Given that, the body slides down from an inclined plane making an angle of 45° with the horizontal, taking time T.

The effective acceleration of the body in this case will be `a = g  sin 45^circ = g/sqrt(2)`

Now for this motion, we can write,

⇒ `s = ut + 1/2  at^2`

That gives us,

⇒ `s = 0*T + 1/2 g/sqrt(2) T^2`

Or ⇒ `s = (gT^2)/(2sqrt(2))`

Now consider the motion of the body along a rough inclined plane, we have

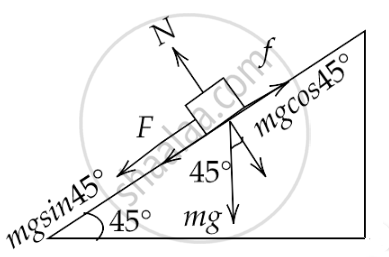
In this case, for the equilibrium condition, we can write

⇒ `ma = mg  sin 45^circ - f`

That gives,

⇒ `ma = (mg)/sqrt(2) - μmg  cos 45^circ`

Or,

⇒ `ma = (mg)/sqrt(2) - μ (mg)/sqrt(2) = (mg)/sqrt(2) (1 - μ)`

Hence ⇒ `a = g/sqrt(2) (1 - μ)`

Now if `t = pT, s = s, a = g/sqrt(2) (1 - μ)`

Then we have

⇒ `s = ut + 1/2 at^2`

That gives,

⇒ `s = 0 * pT + 1/2 g/sqrt(2) (1 - u)p^2T^2`

Or,

⇒ `s = g/(2sqrt(2)) (1 - u) p^2T^2`

Now since the distance in both cases are equal,

Therefore, we have

⇒ `g/(2sqrt(2)) (1 - u)p^2T^2 = (gT^2)/(2sqrt(2))`

That gives us,

⇒ `(1 - u)p^2 = 1`

Or,

⇒ `(1 - u) = 1/p^2`

Hence,

⇒ `u = (1 - 1/p^2)`