Advertisements
Advertisements
प्रश्न
When a body slides down from rest along a smooth inclined plane making an angle of 45° with the horizontal, it takes time T. When the same body slides down from rest along a rough inclined plane making the same angle and through the same distance, it is seen to take time pT, where p is some number greater than 1. Calculate the co-efficient of friction between the body and the rough plane.
उत्तर
Given that, the body slides down from an inclined plane making an angle of 45° with the horizontal, taking time T.
The effective acceleration of the body in this case will be `a = g sin 45^circ = g/sqrt(2)`
Now for this motion, we can write,
⇒ `s = ut + 1/2 at^2`
That gives us,
⇒ `s = 0*T + 1/2 g/sqrt(2) T^2`
Or ⇒ `s = (gT^2)/(2sqrt(2))`
Now consider the motion of the body along a rough inclined plane, we have
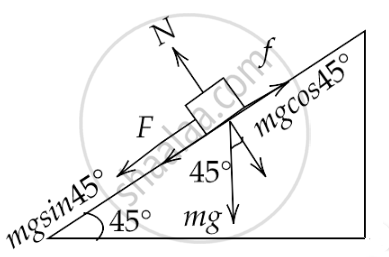
In this case, for the equilibrium condition, we can write
⇒ `ma = mg sin 45^circ - f`
That gives,
⇒ `ma = (mg)/sqrt(2) - μmg cos 45^circ`
Or,
⇒ `ma = (mg)/sqrt(2) - μ (mg)/sqrt(2) = (mg)/sqrt(2) (1 - μ)`
Hence ⇒ `a = g/sqrt(2) (1 - μ)`
Now if `t = pT, s = s, a = g/sqrt(2) (1 - μ)`
Then we have
⇒ `s = ut + 1/2 at^2`
That gives,
⇒ `s = 0 * pT + 1/2 g/sqrt(2) (1 - u)p^2T^2`
Or,
⇒ `s = g/(2sqrt(2)) (1 - u) p^2T^2`
Now since the distance in both cases are equal,
Therefore, we have
⇒ `g/(2sqrt(2)) (1 - u)p^2T^2 = (gT^2)/(2sqrt(2))`
That gives us,
⇒ `(1 - u)p^2 = 1`
Or,
⇒ `(1 - u) = 1/p^2`
Hence,
⇒ `u = (1 - 1/p^2)`
APPEARS IN
संबंधित प्रश्न
A particle is kept fixed on a turntable rotating uniformly. As seen from the ground the particle goes in a circle, its speed is 20 cm/s and acceleration is 20 cm/s2. The particle is now shifted to a new position to make the radius half of the original value. The new value of the speed and acceleration will be
Water in a bucket is whirled in a vertical circle with string attached to it. The water does no fall down even when the bucket is inverted at the top of its path. We conclude that in this position
A rod of length L is pivoted at one end and is rotated with a uniform angular velocity in a horizontal plane. Let T1 and T2 be the tensions at the points L/4 and 3L/4 away from the pivoted ends.
A mosquito is sitting on an L.P. record disc rotating on a turn table at \[33\frac{1}{3}\] revolutions per minute. The distance of the mosquito from the centre of the turn table is 10 cm. Show that the friction coefficient between the record and the mosquito is greater than π2/81. Take g =10 m/s2.
A turn of radius 20 m is banked for the vehicles going at a speed of 36 km/h. If the coefficient of static friction between the road and the tyre is 0.4, what are the possible speeds of a vehicle so that it neither slips down nor skids up?
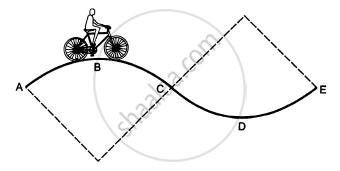
A track consists of two circular parts ABC and CDE of equal radius 100 m and joined smoothly as shown in figure. Each part subtends a right angle at its centre. A cycle weighing 100 kg together with the rider travels at a constant speed of 18 km/h on the track. (a) Find the normal contact force by the road on the cycle when it is at B and at D. (b) Find the force of friction exerted by the track on the tyres when the cycle is at B, C and. (c) Find the normal force between the road and the cycle just before and just after the cycle crosses C. (d) What should be the minimum friction coefficient between the road and the tyre, which will ensure that the cyclist can move with constant speed? Take g = 10 m/s2.
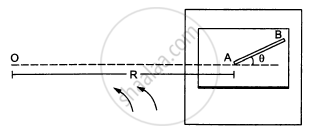
A table with smooth horizontal surface is fixed in a cabin that rotates with a uniform angular velocity ω in a circular path of radius R (In the following figure). A smooth groove AB of length L(<<R) is made the surface of the table. The groove makes an angle θ with the radius OA of the circle in which the cabin rotates. A small particle is kept at the point A in the groove and is released to move at the point A in the groove and is released to move along AB. Find the time taken by the particle to reach the point B.
The escape velocity of a body from any planet, whose mass is six times the mass of earth and radius is twice the radius of earth will be
(v8 = escape velocity of a body from the earth's surface).
A particle performs uniform circular motion in a horizontal plane. The radius of the circle is 10 cm. If the centripetal force F is kept constant but the angular velocity is halved, the new radius of the path will be ______.
A stone tide to a string of length L is whirled in a vertical circle with the other end of the string at the centre. At a certain instant of time, the stone is at its lowest position and has a speed u. The magnitude of change in its velocity, as it reaches a position where the string is horizontal, is `sqrt(x("u"^2 - "gL")`. The value of x is ______.
