Advertisements
Advertisements
Question
When a body slides down from rest along a smooth inclined plane making an angle of 45° with the horizontal, it takes time T. When the same body slides down from rest along a rough inclined plane making the same angle and through the same distance, it is seen to take time pT, where p is some number greater than 1. Calculate the co-efficient of friction between the body and the rough plane.
Solution
Given that, the body slides down from an inclined plane making an angle of 45° with the horizontal, taking time T.
The effective acceleration of the body in this case will be `a = g sin 45^circ = g/sqrt(2)`
Now for this motion, we can write,
⇒ `s = ut + 1/2 at^2`
That gives us,
⇒ `s = 0*T + 1/2 g/sqrt(2) T^2`
Or ⇒ `s = (gT^2)/(2sqrt(2))`
Now consider the motion of the body along a rough inclined plane, we have
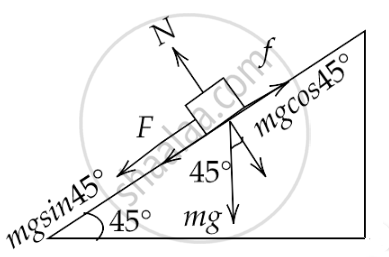
In this case, for the equilibrium condition, we can write
⇒ `ma = mg sin 45^circ - f`
That gives,
⇒ `ma = (mg)/sqrt(2) - μmg cos 45^circ`
Or,
⇒ `ma = (mg)/sqrt(2) - μ (mg)/sqrt(2) = (mg)/sqrt(2) (1 - μ)`
Hence ⇒ `a = g/sqrt(2) (1 - μ)`
Now if `t = pT, s = s, a = g/sqrt(2) (1 - μ)`
Then we have
⇒ `s = ut + 1/2 at^2`
That gives,
⇒ `s = 0 * pT + 1/2 g/sqrt(2) (1 - u)p^2T^2`
Or,
⇒ `s = g/(2sqrt(2)) (1 - u) p^2T^2`
Now since the distance in both cases are equal,
Therefore, we have
⇒ `g/(2sqrt(2)) (1 - u)p^2T^2 = (gT^2)/(2sqrt(2))`
That gives us,
⇒ `(1 - u)p^2 = 1`
Or,
⇒ `(1 - u) = 1/p^2`
Hence,
⇒ `u = (1 - 1/p^2)`
APPEARS IN
RELATED QUESTIONS
A smooth block loosely fits in a circular tube placed on a horizontal surface. The block moves in a uniform circular motion along the tube. Which wall (inner or outer) will exert a nonzero normal contact force on the block?
An object follows a curved path. The following quantities may remain constant during the motion
(a) speed
(b) velocity
(c) acceleration
(d) magnitude of acceleration.
A scooter weighing 150 kg together with its rider moving at 36 km/hr is to take a turn of a radius 30 m. What horizontal force on the scooter is needed to make the turn possible ?
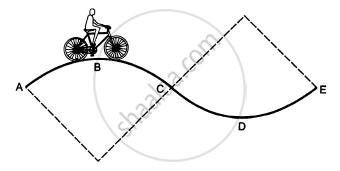
A track consists of two circular parts ABC and CDE of equal radius 100 m and joined smoothly as shown in figure. Each part subtends a right angle at its centre. A cycle weighing 100 kg together with the rider travels at a constant speed of 18 km/h on the track. (a) Find the normal contact force by the road on the cycle when it is at B and at D. (b) Find the force of friction exerted by the track on the tyres when the cycle is at B, C and. (c) Find the normal force between the road and the cycle just before and just after the cycle crosses C. (d) What should be the minimum friction coefficient between the road and the tyre, which will ensure that the cyclist can move with constant speed? Take g = 10 m/s2.
A hemispherical bowl of radius R is rotated about its axis of symmetry which is kept vertical. A small block is kept in the bowl at a position where the radius makes an angle θ with the vertical. The block rotates with the bowl without any slipping. The friction coefficient between the block and the bowl surface is μ. Find the range of the angular speed for which the block will not slip.
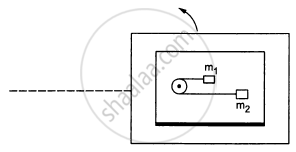
A table with smooth horizontal surface is placed in a circle of a large radius R (In the following figure). A smooth pulley of small radius is fastened to the table. Two masses m and 2m placed on the table are connected through a string going over the pulley. Initially the masses are held by a person with the string along the outward radius and then the system is released from rest (with respect to the cabin). Find the magnitude of the initial acceleration of the masses as seen from the cabin and the tension in the string.
In a certain unit, the radius of gyration of a uniform disc about its central and transverse axis is `sqrt2.5`. Its radius of gyration about a tangent in its plane (in the same unit) must be ______.
Two identical masses are connected to a horizontal thin (massless) rod as shown in the figure. When their distance from the pivot is D, a torque τ produces an angular acceleration of α1. The masses are now repositioned so that they are 2D from the pivot. The same torque produces an angular acceleration α2 which is given by ______
The centripetal force of a body moving in a circular path, if speed is made half and radius is made four times the original value, will ____________.
A person driving a car suddenly applies the brakes on seeing a child on the road ahead. If he is not wearing seat belt, he falls forward and hits his head against the steering wheel. Why?
