Advertisements
Advertisements
Question
A hemispherical bowl of radius R is rotated about its axis of symmetry which is kept vertical. A small block is kept in the bowl at a position where the radius makes an angle θ with the vertical. The block rotates with the bowl without any slipping. The friction coefficient between the block and the bowl surface is μ. Find the range of the angular speed for which the block will not slip.
Solution
When the bowl rotates at maximum angular speed, the block tends to slip upwards.
Also, the frictional force acts downward.
Here, we have:
Radius of the path that the block follow = r = Rsinθ
Let N1 be the normal reaction on the block and ω1 be the angular velocity after which the block will slip.
From the free body diagram-1, we get :
\[N_1 - \text{mg}\cos\theta = {m\omega}_1^2 (R\sin\theta)\sin\theta . . . \](i)
\[\mu N_1 + \text{mg}sin\theta = m \omega_1^2 (R\sin\theta)\cos\theta . . . \](ii)
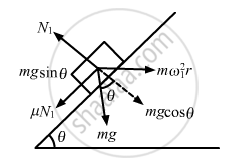
On solving the two equation, we get :
\[\omega_1 = \left[ \frac{g(\text{sin}\theta + \mu\text{ cos}\theta)}{\text{R sin}\theta (\text{cos}\theta - \mu \text{ sin }\theta)} \right]^{1/2}\]
Let us now find the minimum speed (ω2) on altering the direction of \[\mu\] (as shown in figure):
\[\omega_2 = \left[ \frac{g(\text{ sin }\theta - \mu \text{ cos }\theta)}{\text{R sin}\theta (\text{ cos }\theta + \mu \text{ sin }\theta)} \right]^{1/2}\]
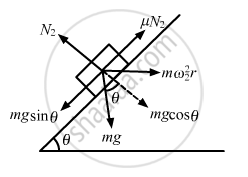
Hence, the range of speed is between ω2 and ω1.
APPEARS IN
RELATED QUESTIONS
An object follows a curved path. The following quantities may remain constant during the motion
(a) speed
(b) velocity
(c) acceleration
(d) magnitude of acceleration.
Assume that the earth goes round the sun in a circular orbit with a constant speed of 30 kms
A car of mass M is moving on a horizontal circular path of radius r. At an instant its speed is v and is increasing at a rate a.
(a) The acceleration of the car is towards the centre of the path.
(b) The magnitude of the frictional force on the car is greater than \[\frac{\text{mv}^2}{\text{r}}\]
(c) The friction coefficient between the ground and the car is not less than a/g.
(d) The friction coefficient between the ground and the car is \[\mu = \tan^{- 1} \frac{\text{v}^2}{\text{rg}.}\]
A stone is fastened to one end of a string and is whirled in a vertical circle of radius R. Find the minimum speed the stone can have at the highest point of the circle.
A mosquito is sitting on an L.P. record disc rotating on a turn table at \[33\frac{1}{3}\] revolutions per minute. The distance of the mosquito from the centre of the turn table is 10 cm. Show that the friction coefficient between the record and the mosquito is greater than π2/81. Take g =10 m/s2.
A simple pendulum is suspended from the ceiling of a car taking a turn of radius 10 m at a speed of 36 km/h. Find the angle made by he string of the pendulum with the vertical if this angle does not change during the turn. Take g = 10 m/s2.
Suppose the amplitude of a simple pendulum having a bob of mass m is θ0. Find the tension in the string when the bob is at its extreme position.
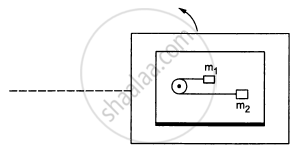
A table with smooth horizontal surface is placed in a circle of a large radius R (In the following figure). A smooth pulley of small radius is fastened to the table. Two masses m and 2m placed on the table are connected through a string going over the pulley. Initially the masses are held by a person with the string along the outward radius and then the system is released from rest (with respect to the cabin). Find the magnitude of the initial acceleration of the masses as seen from the cabin and the tension in the string.
When seen from below, the blades of a ceiling fan are seen to be revolving anticlockwise and their speed is decreasing. Select the correct statement about the directions of its angular velocity and angular acceleration.
A particle of mass 1 kg, tied to a 1.2 m long string is whirled to perform the vertical circular motion, under gravity. The minimum speed of a particle is 5 m/s. Consider the following statements.
P) Maximum speed must be `5sqrt5` m/s.
Q) Difference between maximum and minimum tensions along the string is 60 N.
Select the correct option.
In a certain unit, the radius of gyration of a uniform disc about its central and transverse axis is `sqrt2.5`. Its radius of gyration about a tangent in its plane (in the same unit) must be ______.
A body slides down a smooth inclined plane having angle θ and reaches the bottom with velocity v. If a body is a sphere, then its linear velocity at the bottom of the plane is
Two particles A and B are located at distances rA and rB respectively from the centre of a rotating disc such that rA > rB. In this case, if angular velocity ω of rotation is constant, then ______
A wheel is subjected to uniform angular acceleration about its axis. The wheel is starting from rest and it rotates through an angle θ1, in first two seconds. In the next two seconds, it rotates through an angle θ2. The ratio θ1/θ2 is ____________.
A body of mass m is performing a UCM in a circle of radius r with speed v. The work done by the centripetal force in moving it through `(2/3)`rd of the circular path is ______.
A body is moving along a circular track of radius 100 m with velocity 20 m/s. Its tangential acceleration is 3 m/s2 then its resultant accelaration will be ______.
An engine is moving on a c1rcular path of radius 200 m with speed of 15 m/s. What will be the frequency heard by an observer who is at rest at the centre of the circular path, when engine blows the whistle with frequency 250 Hz?
A person driving a car suddenly applies the brakes on seeing a child on the road ahead. If he is not wearing seat belt, he falls forward and hits his head against the steering wheel. Why?
Which of the following statements is FALSE for a particle moving in a circle with a constant angular speed?
