Advertisements
Advertisements
प्रश्न
A hemispherical bowl of radius R is rotated about its axis of symmetry which is kept vertical. A small block is kept in the bowl at a position where the radius makes an angle θ with the vertical. The block rotates with the bowl without any slipping. The friction coefficient between the block and the bowl surface is μ. Find the range of the angular speed for which the block will not slip.
उत्तर
When the bowl rotates at maximum angular speed, the block tends to slip upwards.
Also, the frictional force acts downward.
Here, we have:
Radius of the path that the block follow = r = Rsinθ
Let N1 be the normal reaction on the block and ω1 be the angular velocity after which the block will slip.
From the free body diagram-1, we get :
\[N_1 - \text{mg}\cos\theta = {m\omega}_1^2 (R\sin\theta)\sin\theta . . . \](i)
\[\mu N_1 + \text{mg}sin\theta = m \omega_1^2 (R\sin\theta)\cos\theta . . . \](ii)
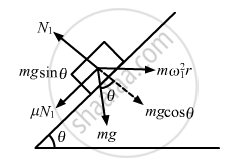
On solving the two equation, we get :
\[\omega_1 = \left[ \frac{g(\text{sin}\theta + \mu\text{ cos}\theta)}{\text{R sin}\theta (\text{cos}\theta - \mu \text{ sin }\theta)} \right]^{1/2}\]
Let us now find the minimum speed (ω2) on altering the direction of \[\mu\] (as shown in figure):
\[\omega_2 = \left[ \frac{g(\text{ sin }\theta - \mu \text{ cos }\theta)}{\text{R sin}\theta (\text{ cos }\theta + \mu \text{ sin }\theta)} \right]^{1/2}\]
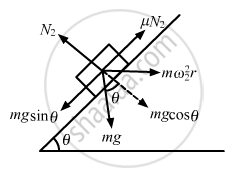
Hence, the range of speed is between ω2 and ω1.
APPEARS IN
संबंधित प्रश्न
A disc revolves with a speed of `33 1/3` rev/min, and has a radius of 15 cm. Two coins are placed at 4 cm and 14 cm away from the centre of the record. If the co-efficient of friction between the coins and the record is 0.15, which of the coins will revolve with the record?
A thin circular loop of radius R rotates about its vertical diameter with an angular frequency ω. Show that a small bead on the wire loop remains at its lowermost point for `omega <= sqrt(g/R)` .What is the angle made by the radius vector joining the centre to the bead with the vertical downward direction for `omega = sqrt("2g"/R)` ?Neglect friction.
A car moves at a constant speed on a road as shown in figure. The normal force by the road on the car NA and NB when it is at the points A and B respectively.

Water in a bucket is whirled in a vertical circle with string attached to it. The water does no fall down even when the bucket is inverted at the top of its path. We conclude that in this position
An object follows a curved path. The following quantities may remain constant during the motion
(a) speed
(b) velocity
(c) acceleration
(d) magnitude of acceleration.
A car of mass M is moving on a horizontal circular path of radius r. At an instant its speed is v and is increasing at a rate a.
(a) The acceleration of the car is towards the centre of the path.
(b) The magnitude of the frictional force on the car is greater than \[\frac{\text{mv}^2}{\text{r}}\]
(c) The friction coefficient between the ground and the car is not less than a/g.
(d) The friction coefficient between the ground and the car is \[\mu = \tan^{- 1} \frac{\text{v}^2}{\text{rg}.}\]
A simple pendulum is suspended from the ceiling of a car taking a turn of radius 10 m at a speed of 36 km/h. Find the angle made by he string of the pendulum with the vertical if this angle does not change during the turn. Take g = 10 m/s2.
A motorcycle has to move with a constant speed on an over bridge which is in the form of a circular arc of radius R and has a total length L. Suppose the motorcycle starts from the highest point.(a) What can its maximum velocity be for which the contact with the road is not broken at the highest point? (b) If the motorcycle goes at speed 1/√2 times the maximum found in part (a), where will it lose the contact with the road? (c) What maximum uniform speed can it maintain on the bridge if it does not lose contact anywhere on the bridge?
A car goes on a horizontal circular road of radius R, the speed increasing at a constant rate \[\frac{\text{dv}}{\text{dt}} = a\] . The friction coefficient between the road and the tyre is μ. Find the speed at which the car will skid.
A particle is projected with a speed u at an angle θ with the horizontal. Consider a small part of its path near the highest position and take it approximately to be a circular arc. What is the radius of this circular circle? This radius is called the radius of curvature of the curve at the point.
When seen from below, the blades of a ceiling fan are seen to be revolving anticlockwise and their speed is decreasing. Select the correct statement about the directions of its angular velocity and angular acceleration.
The real force 'F' acting on a particle of mass ' m' performing circular motion acts along the radius of circle 'r' and is directed towards the centre of circle. The square root of the magnitude of such force is (T = periodic time).
In negotiating curve on a flat road, a cyclist leans inwards by an angle e with the vertical in order to ______.
When a body slides down from rest along a smooth inclined plane making an angle of 45° with the horizontal, it takes time T. When the same body slides down from rest along a rough inclined plane making the same angle and through the same distance, it is seen to take time pT, where p is some number greater than 1. Calculate the co-efficient of friction between the body and the rough plane.
A racing car travels on a track (without banking) ABCDEFA (Figure). ABC is a circular arc of radius 2 R. CD and FA are straight paths of length R and DEF is a circular arc of radius R = 100 m. The co-efficient of friction on the road is µ = 0.1. The maximum speed of the car is 50 ms–1. Find the minimum time for completing one round.

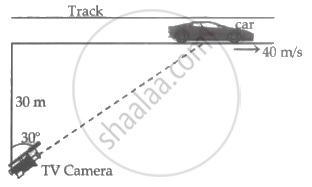
A racing car is travelling along a track at a constant speed of 40 m/s. A T.V. cameraman is recording the event from a distance of 30 m directly away from the track as shown in the figure. In order to keep the car under view in the position shown, the angular speed with which the camera should be rotated is ______.
A stone tide to a string of length L is whirled in a vertical circle with the other end of the string at the centre. At a certain instant of time, the stone is at its lowest position and has a speed u. The magnitude of change in its velocity, as it reaches a position where the string is horizontal, is `sqrt(x("u"^2 - "gL")`. The value of x is ______.
Statement I: A cyclist is moving on an unbanked road with a speed of 7 kmh-1 and takes a sharp circular turn along a path of radius of 2 m without reducing the speed. The static friction coefficient is 0.2. The cyclist will not slip and pass the curve. (g = 9.8 m/s2)
Statement II: If the road is banked at an angle of 45°, cyclist can cross the curve of 2 m radius with the speed of 18.5 kmh-1 without slipping.
In the light of the above statements, choose the correct answer from the options given below.
