Advertisements
Advertisements
प्रश्न
When seen from below, the blades of a ceiling fan are seen to be revolving anticlockwise and their speed is decreasing. Select the correct statement about the directions of its angular velocity and angular acceleration.
पर्याय
Angular velocity upwards, angular acceleration downwards.
Angular velocity downwards, angular acceleration upwards.
Both, angular velocity and angular acceleration, upwards.
Both, angular velocity and angular acceleration, downwards.
उत्तर
Angular velocity downwards, angular acceleration upwards.
Explanation:
As seen below, the fan is rotating in the anticlockwise direction; therefore, by the right-hand thumb rule, the direction of the angular velocity vector is towards the observer. Therefore, the angular velocity vector points downward.
The speed of rotation of the fan decreases in the anticlockwise direction; therefore, the angular acceleration is in the opposite direction. Therefore, the angular acceleration vector points upwards.
APPEARS IN
संबंधित प्रश्न
A disc revolves with a speed of `33 1/3` rev/min, and has a radius of 15 cm. Two coins are placed at 4 cm and 14 cm away from the centre of the record. If the co-efficient of friction between the coins and the record is 0.15, which of the coins will revolve with the record?
A 70 kg man stands in contact against the inner wall of a hollow cylindrical drum of radius 3 m rotating about its vertical axis with 200 rev/min. The coefficient of friction between the wall and his clothing is 0.15. What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed?
When a particle moves in a circle with a uniform speed
A particle is kept fixed on a turntable rotating uniformly. As seen from the ground the particle goes in a circle, its speed is 20 cm/s and acceleration is 20 cm/s2. The particle is now shifted to a new position to make the radius half of the original value. The new value of the speed and acceleration will be
Three identical cars A, B and C are moving at the same speed on three bridges. The car A goes on a place bridge, B on a bridge convex upward and C goes on a bridge concave upward. Let FA, FB and FC be the normal forces exerted by the car on the bridges when they are at the middle of bridges.
A train A runs from east to west and another train B of the same mass runs from west to east at the same speed along the equator. A presses the track with a force F1 and B presses the track with a force F2.
A rod of length L is pivoted at one end and is rotated with a uniform angular velocity in a horizontal plane. Let T1 and T2 be the tensions at the points L/4 and 3L/4 away from the pivoted ends.
The position vector of a particle in a circular motion about the origin sweeps out equal area in equal time. Its
(a) velocity remains constant
(b) speed remains constant
(c) acceleration remains constant
(d) tangential acceleration remains constant.
A particle is going in a spiral path as shown in figure with constant speed.
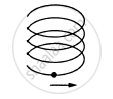
A scooter weighing 150 kg together with its rider moving at 36 km/hr is to take a turn of a radius 30 m. What horizontal force on the scooter is needed to make the turn possible ?
A stone is fastened to one end of a string and is whirled in a vertical circle of radius R. Find the minimum speed the stone can have at the highest point of the circle.
A ceiling fan has a diameter (of the circle through the outer edges of the three blades) of 120 cm and rpm 1500 at full speed. Consider a particle of mass 1 g sticking at the outer end of a blade. How much force does it experience when the fan runs at full speed? Who exerts this force on the particle? How much force does the particle exert on the blade along its surface?
Suppose the bob of the previous problem has a speed of 1.4 m/s when the string makes an angle of 0.20 radian with the vertical. Find the tension at this instant. You can use cos θ ≈ 1 − θ2/2 and SINθ ≈ θ for small θ.
A person stands on a spring balance at the equator. By what fraction is the balance reading less than his true weight?
A turn of radius 20 m is banked for the vehicles going at a speed of 36 km/h. If the coefficient of static friction between the road and the tyre is 0.4, what are the possible speeds of a vehicle so that it neither slips down nor skids up?
A motorcycle has to move with a constant speed on an over bridge which is in the form of a circular arc of radius R and has a total length L. Suppose the motorcycle starts from the highest point.(a) What can its maximum velocity be for which the contact with the road is not broken at the highest point? (b) If the motorcycle goes at speed 1/√2 times the maximum found in part (a), where will it lose the contact with the road? (c) What maximum uniform speed can it maintain on the bridge if it does not lose contact anywhere on the bridge?
A car goes on a horizontal circular road of radius R, the speed increasing at a constant rate \[\frac{\text{dv}}{\text{dt}} = a\] . The friction coefficient between the road and the tyre is μ. Find the speed at which the car will skid.
A particle is projected with a speed u at an angle θ with the horizontal. Consider a small part of its path near the highest position and take it approximately to be a circular arc. What is the radius of this circular circle? This radius is called the radius of curvature of the curve at the point.
What is the radius of curvature of the parabola traced out by the projectile in the previous problem at a point where the particle velocity makes an angle θ/2 with the horizontal?
A table with smooth horizontal surface is fixed in a cabin that rotates with a uniform angular velocity ω in a circular path of radius R (In the following figure). A smooth groove AB of length L(<<R) is made the surface of the table. The groove makes an angle θ with the radius OA of the circle in which the cabin rotates. A small particle is kept at the point A in the groove and is released to move at the point A in the groove and is released to move along AB. Find the time taken by the particle to reach the point B.
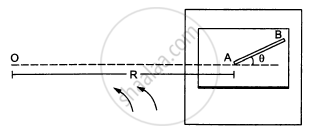
Choose the correct option.
Select correct statement about the formula (expression) of moment of inertia (M.I.) in terms of mass M of the object and some of its distance parameter/s, such as R, L, etc.
A rope is wound around a solid cylinder of mass 1 kg and radius 0.4 m. What is the angular acceleration of cylinder, if the rope is pulled with a force of 25 N? (Cylinder is rotating about its own axis.)
The centripetal force of a body moving in a circular path, if speed is made half and radius is made four times the original value, will ____________.
A rigid body is rotating with angular velocity 'ω' about an axis of rotation. Let 'v' be the linear velocity of particle which is at perpendicular distance 'r' from the axis of rotation. Then the relation 'v = rω' implies that ______.
A body of M.I. 2 kg m2 rotates with an angular velocity of 20 rad/s. When an external torque of 0.5 N m acts on it in the opposite direction, the number of revolutions it makes before it comes to rest is ____________.
A person driving a car suddenly applies the brakes on seeing a child on the road ahead. If he is not wearing seat belt, he falls forward and hits his head against the steering wheel. Why?
Statement I: A cyclist is moving on an unbanked road with a speed of 7 kmh-1 and takes a sharp circular turn along a path of radius of 2 m without reducing the speed. The static friction coefficient is 0.2. The cyclist will not slip and pass the curve. (g = 9.8 m/s2)
Statement II: If the road is banked at an angle of 45°, cyclist can cross the curve of 2 m radius with the speed of 18.5 kmh-1 without slipping.
In the light of the above statements, choose the correct answer from the options given below.
