Advertisements
Advertisements
प्रश्न
A rod of length L is pivoted at one end and is rotated with a uniform angular velocity in a horizontal plane. Let T1 and T2 be the tensions at the points L/4 and 3L/4 away from the pivoted ends.
पर्याय
T1 > T2
T2 > T1
T1 = T2
The relation between T1 and T2 depends on whether the rod rotates clockwise or anticlockwise.
Advertisements
उत्तर
T1 > T2
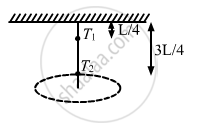
Let the angular velocity of the rod be \[\omega\] .
Distance of the centre of mass of portion of the rod on the right side of L/4 from the pivoted end :
\[r_1 = \frac{L}{4} + \frac{1}{2}\left( \frac{3L}{4} \right) = \frac{5L}{8}\]
Mass of the rod on the right side of L/4 from the pivoted end : \[\text{m}_1 = \frac{3}{4}\text{M}\]
At point L/4, we have :
\[T_1 = \text{ m}_1 \omega^2 \text{ r}_1 \]
\[ = \frac{3}{4}\text{ M } \omega^2 \frac{5}{8}\text{ L} = \frac{15}{32}\text{ M }\omega^2 \text{ L}\]
Distance of the centre of mass of rod on the right side of 3L/4 from the pivoted end :
\[\text{r}_1 = \frac{1}{2}\left( \frac{L}{4} \right) + \frac{3L}{4} = \frac{7L}{8}\]
Mass of the rod on the right side of L/4 from the pivoted end : \[\text{m}_1 = \frac{1}{4}\text{M}\]
At point 3L/4, we have :
\[\text{T}_2 = \text{m}_2 \omega^2 \text{r}_2 \]
\[ = \frac{1}{4}\text{M} \omega^2 \frac{7}{8}\text{L} = \frac{7}{32}\text{M} \omega^2 \text{L}\]
∴ T1 > T2
APPEARS IN
संबंधित प्रश्न
You may have seen in a circus a motorcyclist driving in vertical loops inside a ‘death-well’ (a hollow spherical chamber with holes, so the spectators can watch from outside). Explain clearly why the motorcyclist does not drop down when he is at the uppermost point, with no support from below. What is the minimum speed required at the uppermost position to perform a vertical loop if the radius of the chamber is 25 m?
When a particle moves in a circle with a uniform speed
If the earth stop rotating, the apparent value of g on its surface will
A simple pendulum having a bob of mass m is suspended from the ceiling of a car used in a stunt film shooting. the car moves up along an inclined cliff at a speed v and makes a jump to leave the cliff and lands at some distance. Let R be the maximum height of the car from the top of the cliff. The tension in the string when the car is in air is
Assume that the earth goes round the sun in a circular orbit with a constant speed of 30 kms
The position vector of a particle in a circular motion about the origin sweeps out equal area in equal time. Its
(a) velocity remains constant
(b) speed remains constant
(c) acceleration remains constant
(d) tangential acceleration remains constant.
A mosquito is sitting on an L.P. record disc rotating on a turn table at \[33\frac{1}{3}\] revolutions per minute. The distance of the mosquito from the centre of the turn table is 10 cm. Show that the friction coefficient between the record and the mosquito is greater than π2/81. Take g =10 m/s2.
Suppose the bob of the previous problem has a speed of 1.4 m/s when the string makes an angle of 0.20 radian with the vertical. Find the tension at this instant. You can use cos θ ≈ 1 − θ2/2 and SINθ ≈ θ for small θ.
A person stands on a spring balance at the equator. By what fraction is the balance reading less than his true weight?
A hemispherical bowl of radius R is rotated about its axis of symmetry which is kept vertical. A small block is kept in the bowl at a position where the radius makes an angle θ with the vertical. The block rotates with the bowl without any slipping. The friction coefficient between the block and the bowl surface is μ. Find the range of the angular speed for which the block will not slip.
A particle is projected with a speed u at an angle θ with the horizontal. Consider a small part of its path near the highest position and take it approximately to be a circular arc. What is the radius of this circular circle? This radius is called the radius of curvature of the curve at the point.
A particle of mass 1 kg, tied to a 1.2 m long string is whirled to perform the vertical circular motion, under gravity. The minimum speed of a particle is 5 m/s. Consider the following statements.
P) Maximum speed must be `5sqrt5` m/s.
Q) Difference between maximum and minimum tensions along the string is 60 N.
Select the correct option.
In a certain unit, the radius of gyration of a uniform disc about its central and transverse axis is `sqrt2.5`. Its radius of gyration about a tangent in its plane (in the same unit) must be ______.
In non-uniform circular motion, the ratio of tangential to radial acceleration is (r = radius, a = angular acceleration and v = linear velocity)
A particle of mass m is performing UCM along a circle of radius r. The relation between centripetal acceleration a and kinetic energy E is given by
A body is moving along a circular track of radius 100 m with velocity 20 m/s. Its tangential acceleration is 3 m/s2, then its resultant acceleration will be ______.
Angular displacement (θ) of a flywheel varies with time as θ = at + bt2 + ct3 then angular acceleration is given by ____________.
A particle performs uniform circular motion in a horizontal plane. The radius of the circle is 10 cm. If the centripetal force F is kept constant but the angular velocity is halved, the new radius of the path will be ______.
A body of mass m is performing a UCM in a circle of radius r with speed v. The work done by the centripetal force in moving it through `(2/3)`rd of the circular path is ______.
