Advertisements
Advertisements
प्रश्न
A block of mass m is kept on a horizontal ruler. The friction coefficient between the ruler and the block is μ. The ruler is fixed at one end and the block is at a distance L from the fixed end. The ruler is rotated about the fixed end in the horizontal plane through the fixed end. (a) What can the maximum angular speed be for which the block does not slip? (b) If the angular speed of the ruler is uniformly increased from zero at an angular acceleration α, at what angular speed will the block slip?
Advertisements
उत्तर
(a) Given:
Mass of the block = m
Friction coefficient between the ruler and the block = μ
Let the maximum angular speed be ω1 for which the block does not slip
Now, for the uniform circular motion in the horizontal plane, we have :
\[\mu \text{mg = m }\omega_1^2 L\]
\[ \therefore \omega_1 = \sqrt{\frac{\mu g}{L}}\]
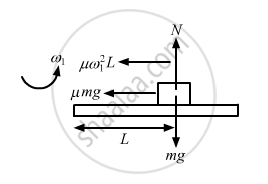
(b) Let the block slip at an angular speed ω2.
For the uniformly accelerated circular motion, we have :
\[\mu \text{mg} = \sqrt{\left( \text{ m }\omega_2^2 L \right)^2 + \left( \text{mL } \alpha^2 \right)^2}\]
\[ \Rightarrow \omega_2^4 + \alpha^2 = \frac{\mu^2 g^2}{L^2}\]
\[\mu \text{mg } = \sqrt{\left( \text{ m }\omega_2^2 L \right)^2 + \left( \text{ mL } \alpha^2 \right)^2}\]
\[ \Rightarrow \omega_2^4 + \alpha^2 = \frac{\mu^2 g^2}{L^2}\]
\[\Rightarrow \omega_2 = \left[ \left( \frac{\mu g}{L} \right)^2 - \alpha^2 \right]^{1/4}\]
APPEARS IN
संबंधित प्रश्न
You may have seen in a circus a motorcyclist driving in vertical loops inside a ‘death-well’ (a hollow spherical chamber with holes, so the spectators can watch from outside). Explain clearly why the motorcyclist does not drop down when he is at the uppermost point, with no support from below. What is the minimum speed required at the uppermost position to perform a vertical loop if the radius of the chamber is 25 m?
A smooth block loosely fits in a circular tube placed on a horizontal surface. The block moves in a uniform circular motion along the tube. Which wall (inner or outer) will exert a nonzero normal contact force on the block?
A car moves at a constant speed on a road as shown in figure. The normal force by the road on the car NA and NB when it is at the points A and B respectively.
A coin placed on a rotating turntable just slips. If it is placed at a distance of 4 cm from the centre. If the angular velocity of the turntable is doubled, it will just slip at a distance of
Three identical cars A, B and C are moving at the same speed on three bridges. The car A goes on a place bridge, B on a bridge convex upward and C goes on a bridge concave upward. Let FA, FB and FC be the normal forces exerted by the car on the bridges when they are at the middle of bridges.
Let θ denote the angular displacement of a simple pendulum oscillating in a vertical plane. If the mass of the bob is m, the tension is the string is mg cos θ
Assume that the earth goes round the sun in a circular orbit with a constant speed of 30 kms
The position vector of a particle in a circular motion about the origin sweeps out equal area in equal time. Its
(a) velocity remains constant
(b) speed remains constant
(c) acceleration remains constant
(d) tangential acceleration remains constant.
A particle is going in a spiral path as shown in figure with constant speed.
Find the acceleration of a particle placed on the surface of the earth at the equator due to earth's rotation. The diameter of earth = 12800 km and it takes 24 hours for the earth to complete one revolution about its axis.
A mosquito is sitting on an L.P. record disc rotating on a turn table at \[33\frac{1}{3}\] revolutions per minute. The distance of the mosquito from the centre of the turn table is 10 cm. Show that the friction coefficient between the record and the mosquito is greater than π2/81. Take g =10 m/s2.
A person stands on a spring balance at the equator. By what fraction is the balance reading less than his true weight?
A motorcycle has to move with a constant speed on an over bridge which is in the form of a circular arc of radius R and has a total length L. Suppose the motorcycle starts from the highest point.(a) What can its maximum velocity be for which the contact with the road is not broken at the highest point? (b) If the motorcycle goes at speed 1/√2 times the maximum found in part (a), where will it lose the contact with the road? (c) What maximum uniform speed can it maintain on the bridge if it does not lose contact anywhere on the bridge?
What is the radius of curvature of the parabola traced out by the projectile in the previous problem at a point where the particle velocity makes an angle θ/2 with the horizontal?
A rope is wound around a solid cylinder of mass 1 kg and radius 0.4 m. What is the angular acceleration of cylinder, if the rope is pulled with a force of 25 N? (Cylinder is rotating about its own axis.)
The real force 'F' acting on a particle of mass ' m' performing circular motion acts along the radius of circle 'r' and is directed towards the centre of circle. The square root of the magnitude of such force is (T = periodic time).
The centripetal force of a body moving in a circular path, if speed is made half and radius is made four times the original value, will ____________.
Which of the following statements is FALSE for a particle moving in a circle with a constant angular speed?
