Advertisements
Advertisements
प्रश्न
A mosquito is sitting on an L.P. record disc rotating on a turn table at \[33\frac{1}{3}\] revolutions per minute. The distance of the mosquito from the centre of the turn table is 10 cm. Show that the friction coefficient between the record and the mosquito is greater than π2/81. Take g =10 m/s2.
उत्तर
\[\text {Frequency of disc = n }= 33\frac{1}{3}\text{ rev/m } = \frac{100}{3 \times 60}\text{rev/s}\]
\[\text { Angular velocity }= \omega = 2\pi n = 2\pi \times \frac{100}{180}=\frac{10\pi}{9}\text{rad/s}\]
r = 10 cm = 0 . 1 m
\[\text{g = 10 m/ s}^2\]
It is given that the mosquito is sitting on the L.P. record disc.Therefore,we have : Friction force ≥ Centrifugal force on the mosquito
⇒ μmg ≥ mrω2
⇒ μ ≥ rω2/g
\[\Rightarrow \mu \geq 0.1\times \left( \frac{10\pi}{9} \right)^2 \frac{1}{10}\]
\[ \Rightarrow \mu \geq \frac{\pi^2}{81}\]
APPEARS IN
संबंधित प्रश्न
A stone of mass 0.25 kg tied to the end of a string is whirled round in a circle of radius 1.5 m with a speed of 40 rev/min in a horizontal plane. What is the tension in the string? What is the maximum speed with which the stone can be whirled around if the string can withstand a maximum tension of 200 N?
A particle is kept fixed on a turntable rotating uniformly. As seen from the ground the particle goes in a circle, its speed is 20 cm/s and acceleration is 20 cm/s2. The particle is now shifted to a new position to make the radius half of the original value. The new value of the speed and acceleration will be
A coin placed on a rotating turntable just slips. If it is placed at a distance of 4 cm from the centre. If the angular velocity of the turntable is doubled, it will just slip at a distance of
A car of mass M is moving on a horizontal circular path of radius r. At an instant its speed is v and is increasing at a rate a.
(a) The acceleration of the car is towards the centre of the path.
(b) The magnitude of the frictional force on the car is greater than \[\frac{\text{mv}^2}{\text{r}}\]
(c) The friction coefficient between the ground and the car is not less than a/g.
(d) The friction coefficient between the ground and the car is \[\mu = \tan^{- 1} \frac{\text{v}^2}{\text{rg}.}\]
Find the acceleration of a particle placed on the surface of the earth at the equator due to earth's rotation. The diameter of earth = 12800 km and it takes 24 hours for the earth to complete one revolution about its axis.
A particle moves in a circle of radius 1.0 cm at a speed given by v = 2.0 t where v is cm/s and t in seconds.
(a) Find the radial acceleration of the particle at t = 1 s.
(b) Find the tangential acceleration at t = 1 s.
(c) Find the magnitude of the acceleration at t = 1 s.
A particle is projected with a speed u at an angle θ with the horizontal. Consider a small part of its path near the highest position and take it approximately to be a circular arc. What is the radius of this circular circle? This radius is called the radius of curvature of the curve at the point.
What is the radius of curvature of the parabola traced out by the projectile in the previous problem at a point where the particle velocity makes an angle θ/2 with the horizontal?
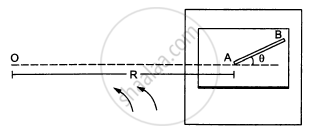
A table with smooth horizontal surface is fixed in a cabin that rotates with a uniform angular velocity ω in a circular path of radius R (In the following figure). A smooth groove AB of length L(<<R) is made the surface of the table. The groove makes an angle θ with the radius OA of the circle in which the cabin rotates. A small particle is kept at the point A in the groove and is released to move at the point A in the groove and is released to move along AB. Find the time taken by the particle to reach the point B.
A person stands on a spring balance at the equator. If the speed of earth's rotation is increased by such an amount that the balance reading is half the true weight, what will be the length of the day in this case?
A particle of mass 1 kg, tied to a 1.2 m long string is whirled to perform the vertical circular motion, under gravity. The minimum speed of a particle is 5 m/s. Consider the following statements.
P) Maximum speed must be `5sqrt5` m/s.
Q) Difference between maximum and minimum tensions along the string is 60 N.
Select the correct option.
In a certain unit, the radius of gyration of a uniform disc about its central and transverse axis is `sqrt2.5`. Its radius of gyration about a tangent in its plane (in the same unit) must be ______.
A particle is moving in a radius R with constant speed v. The magnitude of average acceleration after half revolution is ____________.
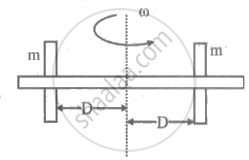
Two identical masses are connected to a horizontal thin (massless) rod as shown in the figure. When their distance from the pivot is D, a torque τ produces an angular acceleration of α1. The masses are now repositioned so that they are 2D from the pivot. The same torque produces an angular acceleration α2 which is given by ______
A rope is wound around a solid cylinder of mass 1 kg and radius 0.4 m. What is the angular acceleration of cylinder, if the rope is pulled with a force of 25 N? (Cylinder is rotating about its own axis.)
An engine requires 5 seconds to go from a speed of 600 r.p.m. to 1200 r.p.m. How many revolutions does it make in this period?
A particle performs uniform circular motion in a horizontal plane. The radius of the circle is 10 cm. If the centripetal force F is kept constant but the angular velocity is halved, the new radius of the path will be ______.
A stone tide to a string of length L is whirled in a vertical circle with the other end of the string at the centre. At a certain instant of time, the stone is at its lowest position and has a speed u. The magnitude of change in its velocity, as it reaches a position where the string is horizontal, is `sqrt(x("u"^2 - "gL")`. The value of x is ______.
