Advertisements
Advertisements
प्रश्न
A coin placed on a rotating turntable just slips. If it is placed at a distance of 4 cm from the centre. If the angular velocity of the turntable is doubled, it will just slip at a distance of
पर्याय
1 cm
2 cm
4 cm
8 cm
उत्तर १
8 cm
उत्तर २
1 cm
Let the force of friction between the coin and the rotating turntable be F.
For the coin to just slip ,
we have : \[\text{ F = m }\omega^2 \text{r}\]
Here, \[\text{ m } \omega^2 \text{ r}\] is the centrifugal force acting on the coin.
For constant F and m, we have : \[\text{r} \propto \frac{1}{\omega^2}\]
Therefore,
\[\frac{\text{r}'}{\text{r}} = \left( \frac{\omega}{\omega'} \right)^2 \]
\[ \Rightarrow \text{ r' = 1 cm }\]
APPEARS IN
संबंधित प्रश्न
A thin circular loop of radius R rotates about its vertical diameter with an angular frequency ω. Show that a small bead on the wire loop remains at its lowermost point for `omega <= sqrt(g/R)` .What is the angle made by the radius vector joining the centre to the bead with the vertical downward direction for `omega = sqrt("2g"/R)` ?Neglect friction.
Three identical cars A, B and C are moving at the same speed on three bridges. The car A goes on a place bridge, B on a bridge convex upward and C goes on a bridge concave upward. Let FA, FB and FC be the normal forces exerted by the car on the bridges when they are at the middle of bridges.
Assume that the earth goes round the sun in a circular orbit with a constant speed of 30 kms
The position vector of a particle in a circular motion about the origin sweeps out equal area in equal time. Its
(a) velocity remains constant
(b) speed remains constant
(c) acceleration remains constant
(d) tangential acceleration remains constant.
A particle is going in a spiral path as shown in figure with constant speed.
A ceiling fan has a diameter (of the circle through the outer edges of the three blades) of 120 cm and rpm 1500 at full speed. Consider a particle of mass 1 g sticking at the outer end of a blade. How much force does it experience when the fan runs at full speed? Who exerts this force on the particle? How much force does the particle exert on the blade along its surface?
A mosquito is sitting on an L.P. record disc rotating on a turn table at \[33\frac{1}{3}\] revolutions per minute. The distance of the mosquito from the centre of the turn table is 10 cm. Show that the friction coefficient between the record and the mosquito is greater than π2/81. Take g =10 m/s2.
The bob of a simple pendulum of length 1 m has mass 100 g and a speed of 1.4 m/s at the lowest point in its path. Find the tension in the string at this instant.
A car goes on a horizontal circular road of radius R, the speed increasing at a constant rate \[\frac{\text{dv}}{\text{dt}} = a\] . The friction coefficient between the road and the tyre is μ. Find the speed at which the car will skid.
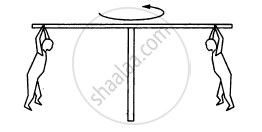
In a children's park a heavy rod is pivoted at the centre and is made to rotate about the pivot so that the rod always remains horizontal. Two kids hold the rod near the ends and thus rotate with the rod (In the following figure). Let the mass of each kid be 15 kg, the distance between the points of the rod where the two kids hold it be 3.0 m and suppose that the rod rotates at the rate of 20 revolutions per minute. Find the force of friction exerted by the rod on one of the kids.
A block of mass m moves on a horizontal circle against the wall of a cylindrical room of radius R. The floor of the room on which the block moves is smooth but the friction coefficient between the wall and the block is μ. The block is given an initial speed v0. As a function of the speed v writes
(a) the normal force by the wall on the block,
(b) the frictional force by a wall, and
(c) the tangential acceleration of the block.
(d) Integrate the tangential acceleration \[\left( \frac{dv}{dt} = v\frac{dv}{ds} \right)\] to obtain the speed of the block after one revolution.
A body is moving along a circular track of radius 100 m with velocity 20 m/s. Its tangential acceleration is 3 m/s2, then its resultant acceleration will be ______.
A body of mass m is performing a UCM in a circle of radius r with speed v. The work done by the centripetal force in moving it through `(2/3)`rd of the circular path is ______.
A body of M.I. 2 kg m2 rotates with an angular velocity of 20 rad/s. When an external torque of 0.5 N m acts on it in the opposite direction, the number of revolutions it makes before it comes to rest is ____________.
An engine is moving on a c1rcular path of radius 200 m with speed of 15 m/s. What will be the frequency heard by an observer who is at rest at the centre of the circular path, when engine blows the whistle with frequency 250 Hz?
A block of 200 g mass moves with a uniform speed in a horizontal circular groove, with vertical side walls of radius 20 cm. If the block takes 40 s to complete one round, the normal force by the side walls of the groove is ______.
Statement I: A cyclist is moving on an unbanked road with a speed of 7 kmh-1 and takes a sharp circular turn along a path of radius of 2 m without reducing the speed. The static friction coefficient is 0.2. The cyclist will not slip and pass the curve. (g = 9.8 m/s2)
Statement II: If the road is banked at an angle of 45°, cyclist can cross the curve of 2 m radius with the speed of 18.5 kmh-1 without slipping.
In the light of the above statements, choose the correct answer from the options given below.
Which of the following statements is FALSE for a particle moving in a circle with a constant angular speed?
Define centripetal force.
