Advertisements
Advertisements
प्रश्न
A thin circular loop of radius R rotates about its vertical diameter with an angular frequency ω. Show that a small bead on the wire loop remains at its lowermost point for `omega <= sqrt(g/R)` .What is the angle made by the radius vector joining the centre to the bead with the vertical downward direction for `omega = sqrt("2g"/R)` ?Neglect friction.
उत्तर १
Let the radius vector joining the bead with the centre make an angle θ, with the vertical downward direction.
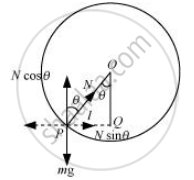
OP = R = Radius of the circle
N = Normal reaction
The respective vertical and horizontal equations of forces can be written as:
mg = Ncosθ ... (i)
mlω2 = Nsinθ … (ii)
In ΔOPQ, we have:
`sin theta = l/R`
`l = Rsin theta`...(iii)
Substiting equation (iii) in equation (ii) we get
m(Rsinθ) ω2 = Nsinθ
mR ω2 = N ... (iv)
Substituting equation (iv) in equation (i), we get:
mg = mR ω2 cosθ
`cos theta = g/(Romega^2)` ...(V)
Since cosθ ≤ 1, the bead will remain at its lowermost point for `g/(Romega^2) <= 1` i.e for `omega <= sqrt(g/R)`
For `omega = sqrt((2g)/R)` or `omega^2 = ((2g)/R)` ..(vi)
On equating equations (v) and (vi), we get:
`(2g)/R = g/(Rcos theta)`
`cos theta = 1/2`
`:. theta = cos^(-1) (0.5 ) = 60^@`
उत्तर २
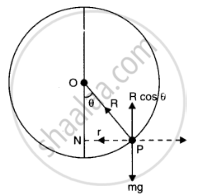
Let the radius vector joining the bead to the centre of the wire make an angle `theta` with the verticle downward dirction. if N is normal reaction, then from fig.
`mg = N cos theta` ....(i)
`mromega^2 = N sin theta` ...(ii)
or `m(R sin theta) omega^2 = N sin theta`
or`mRomega^2 = N`
or `cos theta = g/(Romega^2)`
As |cos theta| <= 1, therefore bead will remain at its lowermost point for
`g/(Romega^2) <= 1 or omega <= sqrt(g/R)`
When `omega = sqrt((2g)/R)` from equation iii
`cos theta = g/R(R/"2g") = 1/2`
`theta = 60^@`
APPEARS IN
संबंधित प्रश्न
A particle is kept fixed on a turntable rotating uniformly. As seen from the ground the particle goes in a circle, its speed is 20 cm/s and acceleration is 20 cm/s2. The particle is now shifted to a new position to make the radius half of the original value. The new value of the speed and acceleration will be
Water in a bucket is whirled in a vertical circle with string attached to it. The water does no fall down even when the bucket is inverted at the top of its path. We conclude that in this position
Find the acceleration of a particle placed on the surface of the earth at the equator due to earth's rotation. The diameter of earth = 12800 km and it takes 24 hours for the earth to complete one revolution about its axis.
A block of mass m is kept on a horizontal ruler. The friction coefficient between the ruler and the block is μ. The ruler is fixed at one end and the block is at a distance L from the fixed end. The ruler is rotated about the fixed end in the horizontal plane through the fixed end. (a) What can the maximum angular speed be for which the block does not slip? (b) If the angular speed of the ruler is uniformly increased from zero at an angular acceleration α, at what angular speed will the block slip?
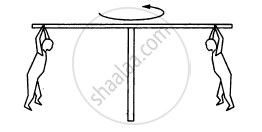
In a children's park a heavy rod is pivoted at the centre and is made to rotate about the pivot so that the rod always remains horizontal. Two kids hold the rod near the ends and thus rotate with the rod (In the following figure). Let the mass of each kid be 15 kg, the distance between the points of the rod where the two kids hold it be 3.0 m and suppose that the rod rotates at the rate of 20 revolutions per minute. Find the force of friction exerted by the rod on one of the kids.
A particle is projected with a speed u at an angle θ with the horizontal. Consider a small part of its path near the highest position and take it approximately to be a circular arc. What is the radius of this circular circle? This radius is called the radius of curvature of the curve at the point.
A wheel is subjected to uniform angular acceleration about its axis. The wheel is starting from rest and it rotates through an angle θ1, in first two seconds. In the next two seconds, it rotates through an angle θ2. The ratio θ1/θ2 is ____________.
A rope is wound around a solid cylinder of mass 1 kg and radius 0.4 m. What is the angular acceleration of cylinder, if the rope is pulled with a force of 25 N? (Cylinder is rotating about its own axis.)
An engine is moving on a c1rcular path of radius 200 m with speed of 15 m/s. What will be the frequency heard by an observer who is at rest at the centre of the circular path, when engine blows the whistle with frequency 250 Hz?
Define centripetal force.
