Advertisements
Advertisements
Question
A thin circular loop of radius R rotates about its vertical diameter with an angular frequency ω. Show that a small bead on the wire loop remains at its lowermost point for `omega <= sqrt(g/R)` .What is the angle made by the radius vector joining the centre to the bead with the vertical downward direction for `omega = sqrt("2g"/R)` ?Neglect friction.
Solution 1
Let the radius vector joining the bead with the centre make an angle θ, with the vertical downward direction.
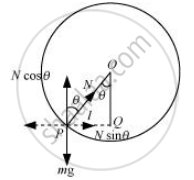
OP = R = Radius of the circle
N = Normal reaction
The respective vertical and horizontal equations of forces can be written as:
mg = Ncosθ ... (i)
mlω2 = Nsinθ … (ii)
In ΔOPQ, we have:
`sin theta = l/R`
`l = Rsin theta`...(iii)
Substiting equation (iii) in equation (ii) we get
m(Rsinθ) ω2 = Nsinθ
mR ω2 = N ... (iv)
Substituting equation (iv) in equation (i), we get:
mg = mR ω2 cosθ
`cos theta = g/(Romega^2)` ...(V)
Since cosθ ≤ 1, the bead will remain at its lowermost point for `g/(Romega^2) <= 1` i.e for `omega <= sqrt(g/R)`
For `omega = sqrt((2g)/R)` or `omega^2 = ((2g)/R)` ..(vi)
On equating equations (v) and (vi), we get:
`(2g)/R = g/(Rcos theta)`
`cos theta = 1/2`
`:. theta = cos^(-1) (0.5 ) = 60^@`
Solution 2
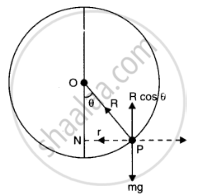
Let the radius vector joining the bead to the centre of the wire make an angle `theta` with the verticle downward dirction. if N is normal reaction, then from fig.
`mg = N cos theta` ....(i)
`mromega^2 = N sin theta` ...(ii)
or `m(R sin theta) omega^2 = N sin theta`
or`mRomega^2 = N`
or `cos theta = g/(Romega^2)`
As |cos theta| <= 1, therefore bead will remain at its lowermost point for
`g/(Romega^2) <= 1 or omega <= sqrt(g/R)`
When `omega = sqrt((2g)/R)` from equation iii
`cos theta = g/R(R/"2g") = 1/2`
`theta = 60^@`
APPEARS IN
RELATED QUESTIONS
A disc revolves with a speed of `33 1/3` rev/min, and has a radius of 15 cm. Two coins are placed at 4 cm and 14 cm away from the centre of the record. If the co-efficient of friction between the coins and the record is 0.15, which of the coins will revolve with the record?
The position vector of a particle in a circular motion about the origin sweeps out equal area in equal time. Its
(a) velocity remains constant
(b) speed remains constant
(c) acceleration remains constant
(d) tangential acceleration remains constant.
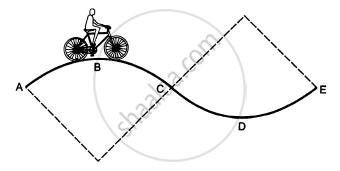
A track consists of two circular parts ABC and CDE of equal radius 100 m and joined smoothly as shown in figure. Each part subtends a right angle at its centre. A cycle weighing 100 kg together with the rider travels at a constant speed of 18 km/h on the track. (a) Find the normal contact force by the road on the cycle when it is at B and at D. (b) Find the force of friction exerted by the track on the tyres when the cycle is at B, C and. (c) Find the normal force between the road and the cycle just before and just after the cycle crosses C. (d) What should be the minimum friction coefficient between the road and the tyre, which will ensure that the cyclist can move with constant speed? Take g = 10 m/s2.
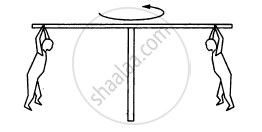
In a children's park a heavy rod is pivoted at the centre and is made to rotate about the pivot so that the rod always remains horizontal. Two kids hold the rod near the ends and thus rotate with the rod (In the following figure). Let the mass of each kid be 15 kg, the distance between the points of the rod where the two kids hold it be 3.0 m and suppose that the rod rotates at the rate of 20 revolutions per minute. Find the force of friction exerted by the rod on one of the kids.
What is the radius of curvature of the parabola traced out by the projectile in the previous problem at a point where the particle velocity makes an angle θ/2 with the horizontal?
A table with smooth horizontal surface is placed in a circle of a large radius R (In the following figure). A smooth pulley of small radius is fastened to the table. Two masses m and 2m placed on the table are connected through a string going over the pulley. Initially the masses are held by a person with the string along the outward radius and then the system is released from rest (with respect to the cabin). Find the magnitude of the initial acceleration of the masses as seen from the cabin and the tension in the string.
A body slides down a smooth inclined plane having angle θ and reaches the bottom with velocity v. If a body is a sphere, then its linear velocity at the bottom of the plane is
Two particles A and B are located at distances rA and rB respectively from the centre of a rotating disc such that rA > rB. In this case, if angular velocity ω of rotation is constant, then ______
Angular displacement (θ) of a flywheel varies with time as θ = at + bt2 + ct3 then angular acceleration is given by ____________.
An engine requires 5 seconds to go from a speed of 600 r.p.m. to 1200 r.p.m. How many revolutions does it make in this period?
