Advertisements
Advertisements
Question
A 70 kg man stands in contact against the inner wall of a hollow cylindrical drum of radius 3 m rotating about its vertical axis with 200 rev/min. The coefficient of friction between the wall and his clothing is 0.15. What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed?
Solution 1
Mass of the man, m = 70 kg
Radius of the drum, r = 3 m
Coefficient of friction, μ = 0.15
Frequency of rotation, ν = 200 rev/min = `200/60 = 10/3 "rev/s"`
The necessary centripetal force required for the rotation of the man is provided by the normal force (FN).
When the floor revolves, the man sticks to the wall of the drum. Hence, the weight of the man (mg) acting downward is balanced by the frictional force
(f = μFN) acting upward.
Hence, the man will not fall until:
mg < f
mg < μFN = μmrω2
g < μrω2
The minimum angular speed is given as:
`omega_"min"= sqrt(g/mu r)`
`= sqrt(10/(0.15 xx 3)) = 4.71 "rad s"^(-1)`
Solution 2
`R = 3m, omega = 200 rev/min = 2xx22/7xx200/60 "rad/s"` `= 440/21 "rad/s"` and `mu = 0.15`
As shown in the figure, the normal reaction (N) of the wall on the man acts in the horizontal direction towards the axis of the cylinder while the force of friction (f) acts vertically upwards. The required centripetal force will be provided by the horizontal reaction N of the wall on the man i.e,
`N = (mv^2)/R = momega^2R`
The frictional force f acting vertically upwards will be balanced by the weight of the man. Hence, the man remains stuck to the wall after the floor is removed if mg ≤ limiting frictional force `f_e` (or `muN`)
or if `mg <= mu m omega^2R`
or `g <= mu omega^2 R`
or `mu omega^2 R >= g or omega >= g/(Rmu)`
Hence, for minimum rotational speed of the cylinder
`omega^2 = g/(muR) = 10/(0.15 xx 3) = 22.2`
`=>omega = sqrt(22.2) = 4.7` rad/s

APPEARS IN
RELATED QUESTIONS
Assume that the earth goes round the sun in a circular orbit with a constant speed of 30 kms
A particle is going in a spiral path as shown in figure with constant speed.
A turn of radius 20 m is banked for the vehicles going at a speed of 36 km/h. If the coefficient of static friction between the road and the tyre is 0.4, what are the possible speeds of a vehicle so that it neither slips down nor skids up?
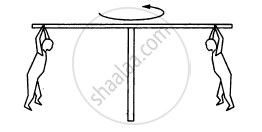
In a children's park a heavy rod is pivoted at the centre and is made to rotate about the pivot so that the rod always remains horizontal. Two kids hold the rod near the ends and thus rotate with the rod (In the following figure). Let the mass of each kid be 15 kg, the distance between the points of the rod where the two kids hold it be 3.0 m and suppose that the rod rotates at the rate of 20 revolutions per minute. Find the force of friction exerted by the rod on one of the kids.
A particle is projected with a speed u at an angle θ with the horizontal. Consider a small part of its path near the highest position and take it approximately to be a circular arc. What is the radius of this circular circle? This radius is called the radius of curvature of the curve at the point.
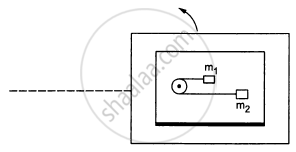
A table with smooth horizontal surface is placed in a circle of a large radius R (In the following figure). A smooth pulley of small radius is fastened to the table. Two masses m and 2m placed on the table are connected through a string going over the pulley. Initially the masses are held by a person with the string along the outward radius and then the system is released from rest (with respect to the cabin). Find the magnitude of the initial acceleration of the masses as seen from the cabin and the tension in the string.
Choose the correct option.
Select correct statement about the formula (expression) of moment of inertia (M.I.) in terms of mass M of the object and some of its distance parameter/s, such as R, L, etc.
A body slides down a smooth inclined plane having angle θ and reaches the bottom with velocity v. If a body is a sphere, then its linear velocity at the bottom of the plane is
An engine is moving on a c1rcular path of radius 200 m with speed of 15 m/s. What will be the frequency heard by an observer who is at rest at the centre of the circular path, when engine blows the whistle with frequency 250 Hz?
Find the angular acceleration of a particle in circular motion which slows down from 300 r.p.m. to 0 r.p.m. in 20 s.
