Advertisements
Advertisements
Question
You may have seen in a circus a motorcyclist driving in vertical loops inside a ‘death-well’ (a hollow spherical chamber with holes, so the spectators can watch from outside). Explain clearly why the motorcyclist does not drop down when he is at the uppermost point, with no support from below. What is the minimum speed required at the uppermost position to perform a vertical loop if the radius of the chamber is 25 m?
Solution 1
When the motorcyclist is at the highest point of the death-well, the normal reaction R on the motorcyclist by the ceiling of the chamber acts downwards. His weight mg also acts downwards. These two forces are balanced by the outward centrifugal force acting on him
:. `R + mg = (mv^2)/r` ......(1)
Here v is the speed of the motorcyclist and m is the mass of the motorcyclist (including the mass of the motorcycle). Because of the balancing of the forces, the motorcyclist does not fall down.
The minimum speed required to perform a vertical loop is given by equation (1) when R = 0.
`:. mg = mv_"min"^2` or `v_"min"^2 = gr`
or `v = sqrt(gr) = sqrt(10xx25) ms^(-1) = 15.8 ms^(-1)`
Solution 2
In a death-well, a motorcyclist does not fall at the top point of a vertical loop because both the force of normal reaction and the weight of the motorcyclist act downward and are balanced by the centripetal force. This situation is shown in the following figure.
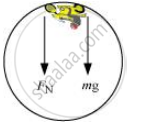
The net force acting on the motorcyclist is the sum of the normal force (FN) and the force due to gravity (Fg = mg).
The equation of motion for the centripetal acceleration ac, can be written as:
Fnet = mac
`F_N + F_g= ma_c`
`F_N + mg =- (mv^2)/r`
Normal reaction is provided by the speed of the motorcyclist. At the minimum speed (vmin), FN = 0
`mg = mv_"min"^2`
`:.V_min = sqrt(rg)`
`= sqrt(25xx10) = 15.8` m/s
APPEARS IN
RELATED QUESTIONS
Water in a bucket is whirled in a vertical circle with string attached to it. The water does no fall down even when the bucket is inverted at the top of its path. We conclude that in this position
A coin placed on a rotating turntable just slips. If it is placed at a distance of 4 cm from the centre. If the angular velocity of the turntable is doubled, it will just slip at a distance of
A train A runs from east to west and another train B of the same mass runs from west to east at the same speed along the equator. A presses the track with a force F1 and B presses the track with a force F2.
A scooter weighing 150 kg together with its rider moving at 36 km/hr is to take a turn of a radius 30 m. What horizontal force on the scooter is needed to make the turn possible ?
Suppose the amplitude of a simple pendulum having a bob of mass m is θ0. Find the tension in the string when the bob is at its extreme position.
A turn of radius 20 m is banked for the vehicles going at a speed of 36 km/h. If the coefficient of static friction between the road and the tyre is 0.4, what are the possible speeds of a vehicle so that it neither slips down nor skids up?
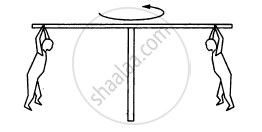
In a children's park a heavy rod is pivoted at the centre and is made to rotate about the pivot so that the rod always remains horizontal. Two kids hold the rod near the ends and thus rotate with the rod (In the following figure). Let the mass of each kid be 15 kg, the distance between the points of the rod where the two kids hold it be 3.0 m and suppose that the rod rotates at the rate of 20 revolutions per minute. Find the force of friction exerted by the rod on one of the kids.
In non-uniform circular motion, the ratio of tangential to radial acceleration is (r = radius, a = angular acceleration and v = linear velocity)
A rigid body is rotating with angular velocity 'ω' about an axis of rotation. Let 'v' be the linear velocity of particle which is at perpendicular distance 'r' from the axis of rotation. Then the relation 'v = rω' implies that ______.
A person driving a car suddenly applies the brakes on seeing a child on the road ahead. If he is not wearing seat belt, he falls forward and hits his head against the steering wheel. Why?
