Advertisements
Advertisements
प्रश्न
You may have seen in a circus a motorcyclist driving in vertical loops inside a ‘death-well’ (a hollow spherical chamber with holes, so the spectators can watch from outside). Explain clearly why the motorcyclist does not drop down when he is at the uppermost point, with no support from below. What is the minimum speed required at the uppermost position to perform a vertical loop if the radius of the chamber is 25 m?
उत्तर १
When the motorcyclist is at the highest point of the death-well, the normal reaction R on the motorcyclist by the ceiling of the chamber acts downwards. His weight mg also acts downwards. These two forces are balanced by the outward centrifugal force acting on him
:. `R + mg = (mv^2)/r` ......(1)
Here v is the speed of the motorcyclist and m is the mass of the motorcyclist (including the mass of the motorcycle). Because of the balancing of the forces, the motorcyclist does not fall down.
The minimum speed required to perform a vertical loop is given by equation (1) when R = 0.
`:. mg = mv_"min"^2` or `v_"min"^2 = gr`
or `v = sqrt(gr) = sqrt(10xx25) ms^(-1) = 15.8 ms^(-1)`
उत्तर २
In a death-well, a motorcyclist does not fall at the top point of a vertical loop because both the force of normal reaction and the weight of the motorcyclist act downward and are balanced by the centripetal force. This situation is shown in the following figure.
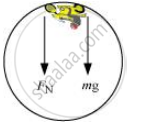
The net force acting on the motorcyclist is the sum of the normal force (FN) and the force due to gravity (Fg = mg).
The equation of motion for the centripetal acceleration ac, can be written as:
Fnet = mac
`F_N + F_g= ma_c`
`F_N + mg =- (mv^2)/r`
Normal reaction is provided by the speed of the motorcyclist. At the minimum speed (vmin), FN = 0
`mg = mv_"min"^2`
`:.V_min = sqrt(rg)`
`= sqrt(25xx10) = 15.8` m/s
APPEARS IN
संबंधित प्रश्न
Water in a bucket is whirled in a vertical circle with string attached to it. The water does no fall down even when the bucket is inverted at the top of its path. We conclude that in this position
A coin placed on a rotating turntable just slips. If it is placed at a distance of 4 cm from the centre. If the angular velocity of the turntable is doubled, it will just slip at a distance of
A car of mass M is moving on a horizontal circular path of radius r. At an instant its speed is v and is increasing at a rate a.
(a) The acceleration of the car is towards the centre of the path.
(b) The magnitude of the frictional force on the car is greater than \[\frac{\text{mv}^2}{\text{r}}\]
(c) The friction coefficient between the ground and the car is not less than a/g.
(d) The friction coefficient between the ground and the car is \[\mu = \tan^{- 1} \frac{\text{v}^2}{\text{rg}.}\]
What is the radius of curvature of the parabola traced out by the projectile in the previous problem at a point where the particle velocity makes an angle θ/2 with the horizontal?
A block of mass m moves on a horizontal circle against the wall of a cylindrical room of radius R. The floor of the room on which the block moves is smooth but the friction coefficient between the wall and the block is μ. The block is given an initial speed v0. As a function of the speed v writes
(a) the normal force by the wall on the block,
(b) the frictional force by a wall, and
(c) the tangential acceleration of the block.
(d) Integrate the tangential acceleration \[\left( \frac{dv}{dt} = v\frac{dv}{ds} \right)\] to obtain the speed of the block after one revolution.
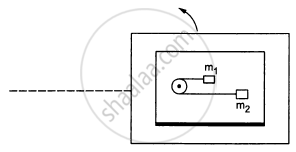
A table with smooth horizontal surface is placed in a circle of a large radius R (In the following figure). A smooth pulley of small radius is fastened to the table. Two masses m and 2m placed on the table are connected through a string going over the pulley. Initially the masses are held by a person with the string along the outward radius and then the system is released from rest (with respect to the cabin). Find the magnitude of the initial acceleration of the masses as seen from the cabin and the tension in the string.
A rope is wound around a solid cylinder of mass 1 kg and radius 0.4 m. What is the angular acceleration of cylinder, if the rope is pulled with a force of 25 N? (Cylinder is rotating about its own axis.)
A body of mass m is performing a UCM in a circle of radius r with speed v. The work done by the centripetal force in moving it through `(2/3)`rd of the circular path is ______.
A person driving a car suddenly applies the brakes on seeing a child on the road ahead. If he is not wearing seat belt, he falls forward and hits his head against the steering wheel. Why?
Find the angular acceleration of a particle in circular motion which slows down from 300 r.p.m. to 0 r.p.m. in 20 s.
