Advertisements
Advertisements
प्रश्न
You may have seen in a circus a motorcyclist driving in vertical loops inside a ‘death-well’ (a hollow spherical chamber with holes, so the spectators can watch from outside). Explain clearly why the motorcyclist does not drop down when he is at the uppermost point, with no support from below. What is the minimum speed required at the uppermost position to perform a vertical loop if the radius of the chamber is 25 m?
उत्तर १
When the motorcyclist is at the highest point of the death-well, the normal reaction R on the motorcyclist by the ceiling of the chamber acts downwards. His weight mg also acts downwards. These two forces are balanced by the outward centrifugal force acting on him
:. `R + mg = (mv^2)/r` ......(1)
Here v is the speed of the motorcyclist and m is the mass of the motorcyclist (including the mass of the motorcycle). Because of the balancing of the forces, the motorcyclist does not fall down.
The minimum speed required to perform a vertical loop is given by equation (1) when R = 0.
`:. mg = mv_"min"^2` or `v_"min"^2 = gr`
or `v = sqrt(gr) = sqrt(10xx25) ms^(-1) = 15.8 ms^(-1)`
उत्तर २
In a death-well, a motorcyclist does not fall at the top point of a vertical loop because both the force of normal reaction and the weight of the motorcyclist act downward and are balanced by the centripetal force. This situation is shown in the following figure.
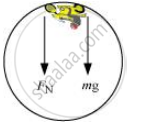
The net force acting on the motorcyclist is the sum of the normal force (FN) and the force due to gravity (Fg = mg).
The equation of motion for the centripetal acceleration ac, can be written as:
Fnet = mac
`F_N + F_g= ma_c`
`F_N + mg =- (mv^2)/r`
Normal reaction is provided by the speed of the motorcyclist. At the minimum speed (vmin), FN = 0
`mg = mv_"min"^2`
`:.V_min = sqrt(rg)`
`= sqrt(25xx10) = 15.8` m/s
APPEARS IN
संबंधित प्रश्न
A coin placed on a rotating turntable just slips. If it is placed at a distance of 4 cm from the centre. If the angular velocity of the turntable is doubled, it will just slip at a distance of
The bob of a simple pendulum of length 1 m has mass 100 g and a speed of 1.4 m/s at the lowest point in its path. Find the tension in the string at this instant.
A car goes on a horizontal circular road of radius R, the speed increasing at a constant rate \[\frac{\text{dv}}{\text{dt}} = a\] . The friction coefficient between the road and the tyre is μ. Find the speed at which the car will skid.
In non-uniform circular motion, the ratio of tangential to radial acceleration is (r = radius, a = angular acceleration and v = linear velocity)
A particle is moving in a radius R with constant speed v. The magnitude of average acceleration after half revolution is ____________.
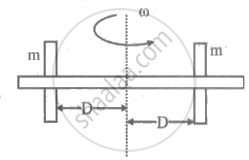
Two identical masses are connected to a horizontal thin (massless) rod as shown in the figure. When their distance from the pivot is D, a torque τ produces an angular acceleration of α1. The masses are now repositioned so that they are 2D from the pivot. The same torque produces an angular acceleration α2 which is given by ______
The escape velocity of a body from any planet, whose mass is six times the mass of earth and radius is twice the radius of earth will be
(v8 = escape velocity of a body from the earth's surface).
A rigid body is rotating with angular velocity 'ω' about an axis of rotation. Let 'v' be the linear velocity of particle which is at perpendicular distance 'r' from the axis of rotation. Then the relation 'v = rω' implies that ______.
An engine is moving on a c1rcular path of radius 200 m with speed of 15 m/s. What will be the frequency heard by an observer who is at rest at the centre of the circular path, when engine blows the whistle with frequency 250 Hz?
Which of the following statements is FALSE for a particle moving in a circle with a constant angular speed?
