Advertisements
Advertisements
प्रश्न
A disc revolves with a speed of `33 1/3` rev/min, and has a radius of 15 cm. Two coins are placed at 4 cm and 14 cm away from the centre of the record. If the co-efficient of friction between the coins and the record is 0.15, which of the coins will revolve with the record?
उत्तर १
If the coin is to revolve with the record, then the force of friction must be enough to provide the necessary centripetal force
`:. mr omega^2 <= mu_s mg` or `r <= (mu_s mg)/(m omega^2)` or `r <= (mu_sg)/omega^2`
frequency = `33 1/2 "rpm"` = `100/3 "rpm" = 100/(3xx60) "rps"`
The Problems in which centripetal force is obtained fromforce of friction, start with the follwoing equation:
`m romega^2 <= mu_s mg`
`omega = 2pi xx 100/(3xx60)"rad s"^(-1) = 10/9 pi rad s^(-1)`
`(mu_sg)/omega^2 = (0.15xx10)/(10/9 pi)^2 m = 0.12 m = 12 cm`
The condition (r < = 12 cm) is satified by the coin placed at 4 cm from the centre of record. So the coin at 4 cm will revolve with the record.
उत्तर २
Coin placed at 4 cm from the centre
Mass of each coin = m
Radius of the disc, r = 15 cm = 0.15 m
Frequency of revolution, v = `33 1/3` rev/min = `100/ (3xx60) = 5/9 "rev/s"`
Coefficient of friction, μ = 0.15
In the given situation, the coin having a force of friction greater than or equal to the centripetal force provided by the rotation of the disc will revolve with the disc. If this is not the case, then the coin will slip from the disc.
Coin placed at 4 cm:
Radius of revolution, r' = 4 cm = 0.04 m
Angular frequency, ω = 2πν = `2 xx 22/7 xx 5/9 = 3.49 s^(-1)`
Frictional force, f = μmg = 0.15 × m × 10 = 1.5m N
Centripetal force on the coin:
`F_"cent" = mr^'omega^2`
`= m xx 0.04 xx (3.49)^2`
= 0.49 m N
Since f > Fcent, the coin will revolve along with the record.
Coin placed at 14 cm:
Radius, `r^n` = 14 cm = 0.14 m
Angular frequency, ω = 3.49 s–1
Frictional force, f' = 1.5m N
Centripetal force is given as:
`F_"cent" = mr^"` `omega^2`
= m × 0.14 × (3.49)2
= 1.7m N
Since f < Fcent., the coin will slip from the surface of the record.
APPEARS IN
संबंधित प्रश्न
A 70 kg man stands in contact against the inner wall of a hollow cylindrical drum of radius 3 m rotating about its vertical axis with 200 rev/min. The coefficient of friction between the wall and his clothing is 0.15. What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed?
A rod of length L is pivoted at one end and is rotated with a uniform angular velocity in a horizontal plane. Let T1 and T2 be the tensions at the points L/4 and 3L/4 away from the pivoted ends.
An object follows a curved path. The following quantities may remain constant during the motion
(a) speed
(b) velocity
(c) acceleration
(d) magnitude of acceleration.
Find the acceleration of a particle placed on the surface of the earth at the equator due to earth's rotation. The diameter of earth = 12800 km and it takes 24 hours for the earth to complete one revolution about its axis.
A particle moves in a circle of radius 1.0 cm at a speed given by v = 2.0 t where v is cm/s and t in seconds.
(a) Find the radial acceleration of the particle at t = 1 s.
(b) Find the tangential acceleration at t = 1 s.
(c) Find the magnitude of the acceleration at t = 1 s.
A person stands on a spring balance at the equator. By what fraction is the balance reading less than his true weight?
A block of mass m moves on a horizontal circle against the wall of a cylindrical room of radius R. The floor of the room on which the block moves is smooth but the friction coefficient between the wall and the block is μ. The block is given an initial speed v0. As a function of the speed v writes
(a) the normal force by the wall on the block,
(b) the frictional force by a wall, and
(c) the tangential acceleration of the block.
(d) Integrate the tangential acceleration \[\left( \frac{dv}{dt} = v\frac{dv}{ds} \right)\] to obtain the speed of the block after one revolution.
An engine is moving on a c1rcular path of radius 200 m with speed of 15 m/s. What will be the frequency heard by an observer who is at rest at the centre of the circular path, when engine blows the whistle with frequency 250 Hz?
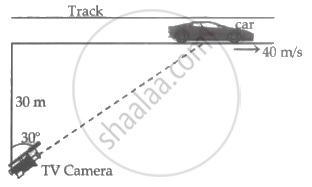
A racing car is travelling along a track at a constant speed of 40 m/s. A T.V. cameraman is recording the event from a distance of 30 m directly away from the track as shown in the figure. In order to keep the car under view in the position shown, the angular speed with which the camera should be rotated is ______.
Find the angular acceleration of a particle in circular motion which slows down from 300 r.p.m. to 0 r.p.m. in 20 s.
