Advertisements
Advertisements
प्रश्न
A block of mass m moves on a horizontal circle against the wall of a cylindrical room of radius R. The floor of the room on which the block moves is smooth but the friction coefficient between the wall and the block is μ. The block is given an initial speed v0. As a function of the speed v writes
(a) the normal force by the wall on the block,
(b) the frictional force by a wall, and
(c) the tangential acceleration of the block.
(d) Integrate the tangential acceleration \[\left( \frac{dv}{dt} = v\frac{dv}{ds} \right)\] to obtain the speed of the block after one revolution.
उत्तर
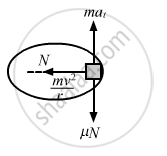
Given:
Radius of the room = R
Mass of the block = m
(a) Normal reaction by the wall on the block = N = \[\frac{m v^2}{R}\]
(b) Force of frictional by the wall = \[\mu N = \frac{\mu m v^2}{R}\]
(c) Let at be the tangential acceleration of the block.
From figure, we get :
\[- \frac{\mu m v^2}{R} = m a_t \]
\[ \Rightarrow a_t = - \frac{\mu v^2}{R}\]
(d) \[\text { On using a }= \frac{dv}{dt} = v\frac{dv}{ds}, \text { we get : } \]
\[v\frac{dv}{ds} = \frac{\mu v^2}{R}\]
\[ \Rightarrow ds = - \frac{R}{\mu}\frac{dv}{v}\]
\[\text { Integrating both side, we get : } \]
\[s = - \frac{R}{\mu}\text{In v + c }\]
\[\text{ At, s = 0, v = v}_0 \]
\[\text{ So, c} = \frac{R}{\mu}\text{ In v}_0 \]
\[ \Rightarrow s = - \frac{R}{\mu}\text{ In}\frac{v}{v_0}\]
\[ \Rightarrow \frac{v}{\text{v}_0} = e^{- \frac{\mu \text{s}}{R}} \]
\[ \Rightarrow \text{v = v}_0 e^{- \frac{\mu s}{R}} \]
\[\text { For one rotation }, \text { we have : }\]
\[s = 2\pi r\]
\[ \therefore \text{v = v}_0 e^{- 2\pi\mu} \]
APPEARS IN
संबंधित प्रश्न
A car moves at a constant speed on a road as shown in figure. The normal force by the road on the car NA and NB when it is at the points A and B respectively.

A stone of mass m tied to a string of length l is rotated in a circle with the other end of the string as the centre. The speed of the stone is v. If the string breaks, the stone will move
A motorcycle is going on an overbridge of radius R. The driver maintains a constant speed. As the motorcycle is ascending on the overbridge, the normal force on it
Three identical cars A, B and C are moving at the same speed on three bridges. The car A goes on a place bridge, B on a bridge convex upward and C goes on a bridge concave upward. Let FA, FB and FC be the normal forces exerted by the car on the bridges when they are at the middle of bridges.
An object follows a curved path. The following quantities may remain constant during the motion
(a) speed
(b) velocity
(c) acceleration
(d) magnitude of acceleration.
A particle is going in a spiral path as shown in figure with constant speed.
Find the acceleration of the moon with respect to the earth from the following data:
Distance between the earth and the moon = 3.85 × 105 km and the time taken by the moon to complete one revolution around the earth = 27.3 days.
Suppose the amplitude of a simple pendulum having a bob of mass m is θ0. Find the tension in the string when the bob is at its extreme position.
A motorcycle has to move with a constant speed on an over bridge which is in the form of a circular arc of radius R and has a total length L. Suppose the motorcycle starts from the highest point.(a) What can its maximum velocity be for which the contact with the road is not broken at the highest point? (b) If the motorcycle goes at speed 1/√2 times the maximum found in part (a), where will it lose the contact with the road? (c) What maximum uniform speed can it maintain on the bridge if it does not lose contact anywhere on the bridge?
A car goes on a horizontal circular road of radius R, the speed increasing at a constant rate \[\frac{\text{dv}}{\text{dt}} = a\] . The friction coefficient between the road and the tyre is μ. Find the speed at which the car will skid.
A block of mass m is kept on a horizontal ruler. The friction coefficient between the ruler and the block is μ. The ruler is fixed at one end and the block is at a distance L from the fixed end. The ruler is rotated about the fixed end in the horizontal plane through the fixed end. (a) What can the maximum angular speed be for which the block does not slip? (b) If the angular speed of the ruler is uniformly increased from zero at an angular acceleration α, at what angular speed will the block slip?
A person stands on a spring balance at the equator. If the speed of earth's rotation is increased by such an amount that the balance reading is half the true weight, what will be the length of the day in this case?
Choose the correct option.
Select correct statement about the formula (expression) of moment of inertia (M.I.) in terms of mass M of the object and some of its distance parameter/s, such as R, L, etc.
In a certain unit, the radius of gyration of a uniform disc about its central and transverse axis is `sqrt2.5`. Its radius of gyration about a tangent in its plane (in the same unit) must be ______.
Two particles A and B are located at distances rA and rB respectively from the centre of a rotating disc such that rA > rB. In this case, if angular velocity ω of rotation is constant, then ______
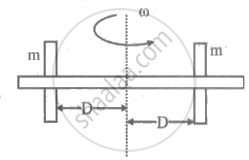
Two identical masses are connected to a horizontal thin (massless) rod as shown in the figure. When their distance from the pivot is D, a torque τ produces an angular acceleration of α1. The masses are now repositioned so that they are 2D from the pivot. The same torque produces an angular acceleration α2 which is given by ______
A body is moving along a circular track of radius 100 m with velocity 20 m/s. Its tangential acceleration is 3 m/s2, then its resultant acceleration will be ______.
If a cyclist doubles his speed while negotiating a curve, how does the tendency to overturn vary?
A body of M.I. 2 kg m2 rotates with an angular velocity of 20 rad/s. When an external torque of 0.5 N m acts on it in the opposite direction, the number of revolutions it makes before it comes to rest is ____________.
A stone tide to a string of length L is whirled in a vertical circle with the other end of the string at the centre. At a certain instant of time, the stone is at its lowest position and has a speed u. The magnitude of change in its velocity, as it reaches a position where the string is horizontal, is `sqrt(x("u"^2 - "gL")`. The value of x is ______.
