Advertisements
Advertisements
Question
A block of mass m moves on a horizontal circle against the wall of a cylindrical room of radius R. The floor of the room on which the block moves is smooth but the friction coefficient between the wall and the block is μ. The block is given an initial speed v0. As a function of the speed v writes
(a) the normal force by the wall on the block,
(b) the frictional force by a wall, and
(c) the tangential acceleration of the block.
(d) Integrate the tangential acceleration \[\left( \frac{dv}{dt} = v\frac{dv}{ds} \right)\] to obtain the speed of the block after one revolution.
Solution
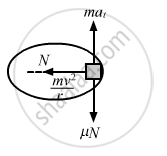
Given:
Radius of the room = R
Mass of the block = m
(a) Normal reaction by the wall on the block = N = \[\frac{m v^2}{R}\]
(b) Force of frictional by the wall = \[\mu N = \frac{\mu m v^2}{R}\]
(c) Let at be the tangential acceleration of the block.
From figure, we get :
\[- \frac{\mu m v^2}{R} = m a_t \]
\[ \Rightarrow a_t = - \frac{\mu v^2}{R}\]
(d) \[\text { On using a }= \frac{dv}{dt} = v\frac{dv}{ds}, \text { we get : } \]
\[v\frac{dv}{ds} = \frac{\mu v^2}{R}\]
\[ \Rightarrow ds = - \frac{R}{\mu}\frac{dv}{v}\]
\[\text { Integrating both side, we get : } \]
\[s = - \frac{R}{\mu}\text{In v + c }\]
\[\text{ At, s = 0, v = v}_0 \]
\[\text{ So, c} = \frac{R}{\mu}\text{ In v}_0 \]
\[ \Rightarrow s = - \frac{R}{\mu}\text{ In}\frac{v}{v_0}\]
\[ \Rightarrow \frac{v}{\text{v}_0} = e^{- \frac{\mu \text{s}}{R}} \]
\[ \Rightarrow \text{v = v}_0 e^{- \frac{\mu s}{R}} \]
\[\text { For one rotation }, \text { we have : }\]
\[s = 2\pi r\]
\[ \therefore \text{v = v}_0 e^{- 2\pi\mu} \]
APPEARS IN
RELATED QUESTIONS
A smooth block loosely fits in a circular tube placed on a horizontal surface. The block moves in a uniform circular motion along the tube. Which wall (inner or outer) will exert a nonzero normal contact force on the block?
A train A runs from east to west and another train B of the same mass runs from west to east at the same speed along the equator. A presses the track with a force F1 and B presses the track with a force F2.
An object follows a curved path. The following quantities may remain constant during the motion
(a) speed
(b) velocity
(c) acceleration
(d) magnitude of acceleration.
The position vector of a particle in a circular motion about the origin sweeps out equal area in equal time. Its
(a) velocity remains constant
(b) speed remains constant
(c) acceleration remains constant
(d) tangential acceleration remains constant.
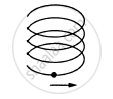
A particle is going in a spiral path as shown in figure with constant speed.
A mosquito is sitting on an L.P. record disc rotating on a turn table at \[33\frac{1}{3}\] revolutions per minute. The distance of the mosquito from the centre of the turn table is 10 cm. Show that the friction coefficient between the record and the mosquito is greater than π2/81. Take g =10 m/s2.
A car goes on a horizontal circular road of radius R, the speed increasing at a constant rate \[\frac{\text{dv}}{\text{dt}} = a\] . The friction coefficient between the road and the tyre is μ. Find the speed at which the car will skid.
What is the radius of curvature of the parabola traced out by the projectile in the previous problem at a point where the particle velocity makes an angle θ/2 with the horizontal?
When seen from below, the blades of a ceiling fan are seen to be revolving anticlockwise and their speed is decreasing. Select the correct statement about the directions of its angular velocity and angular acceleration.
A particle of mass 1 kg, tied to a 1.2 m long string is whirled to perform the vertical circular motion, under gravity. The minimum speed of a particle is 5 m/s. Consider the following statements.
P) Maximum speed must be `5sqrt5` m/s.
Q) Difference between maximum and minimum tensions along the string is 60 N.
Select the correct option.
A body slides down a smooth inclined plane having angle θ and reaches the bottom with velocity v. If a body is a sphere, then its linear velocity at the bottom of the plane is
A body is moving along a circular track of radius 100 m with velocity 20 m/s. Its tangential acceleration is 3 m/s2, then its resultant acceleration will be ______.
Angular displacement (θ) of a flywheel varies with time as θ = at + bt2 + ct3 then angular acceleration is given by ____________.
An engine requires 5 seconds to go from a speed of 600 r.p.m. to 1200 r.p.m. How many revolutions does it make in this period?
A particle performs uniform circular motion in a horizontal plane. The radius of the circle is 10 cm. If the centripetal force F is kept constant but the angular velocity is halved, the new radius of the path will be ______.
An engine is moving on a c1rcular path of radius 200 m with speed of 15 m/s. What will be the frequency heard by an observer who is at rest at the centre of the circular path, when engine blows the whistle with frequency 250 Hz?
A racing car travels on a track (without banking) ABCDEFA (Figure). ABC is a circular arc of radius 2 R. CD and FA are straight paths of length R and DEF is a circular arc of radius R = 100 m. The co-efficient of friction on the road is µ = 0.1. The maximum speed of the car is 50 ms–1. Find the minimum time for completing one round.

A block of 200 g mass moves with a uniform speed in a horizontal circular groove, with vertical side walls of radius 20 cm. If the block takes 40 s to complete one round, the normal force by the side walls of the groove is ______.
