Question

A car goes on a horizontal circular road of radius R, the speed increasing at a constant rate \[\frac{\text{dv}}{\text{dt}} = a\] . The friction coefficient between the road and the tyre is μ. Find the speed at which the car will skid.

Answer 1

Let v be the speed of the car.
Since the motion is non-uniform, the acceleration has both radial (a_r) and tangential (a_t) components.

\[\text{a}_\text{r} = \frac{\text{v}^2}{\text{R}}\] 

\[ \text{a}_\text{t} = \frac{\text{dv}}{\text{dt}} = a\]

\[\text { Resultant magnitude } = \sqrt{\left( \frac{\text{v}^2}{R} \right)^2 + a^2}\]

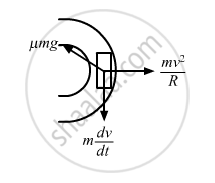
From free body diagram, we have :

\[\text{mN = m}\sqrt{\left( \frac{\text{v}^2}{R} \right)^2 + a^2}\]

\[ \Rightarrow \mu \text{ mg = m}\sqrt{\left( \frac{\text{v}^2}{R} \right)^2 + a^2}\]

\[ \Rightarrow \mu^2 g^2 = \frac{\text{v}^4}{R^2} + a^2\]

\[\Rightarrow \frac{\text{v}^4}{R^2} = ( \mu^2 g^2 - a^2 )\]

\[ \Rightarrow \text{v}^4 = ( \mu^2 g^2 - a^2 ) R^2 \]

\[ \Rightarrow \text{v} = [( \mu^2 g^2 - a^2 ) R^2 ]^{1/4}\]