Advertisements
Advertisements
Question
A motorcycle has to move with a constant speed on an over bridge which is in the form of a circular arc of radius R and has a total length L. Suppose the motorcycle starts from the highest point.(a) What can its maximum velocity be for which the contact with the road is not broken at the highest point? (b) If the motorcycle goes at speed 1/√2 times the maximum found in part (a), where will it lose the contact with the road? (c) What maximum uniform speed can it maintain on the bridge if it does not lose contact anywhere on the bridge?
Solution
R = Radius of the bridge
L = Total length of the over bridge
(a) At the highest point:
Let m be the mass of the motorcycle and v be the required velocity.
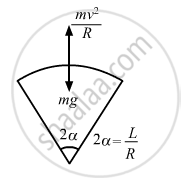
\[\text{mg }= \frac{\text{mv}^2}{\text{R}}\]
\[ \Rightarrow \text{v}^2 = \text{Rg}\]
\[ \Rightarrow \text{v} = \sqrt{\text{Rrg}}\]
\[\left( b \right) \text {Given :} \]
\[ \text{v} = \left( \frac{1}{\sqrt{2}} \right)\sqrt{\text{Rg}}\]
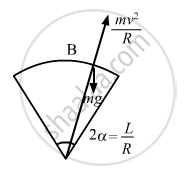
Suppose it loses contact at B.
\[\text {At point B, we get : }\]
\[\text{mg}\cos\theta = \frac{\text{mv}^2}{R}\]
\[ \Rightarrow \text{v}^2 = \text{Rg}\cos\theta\]
\[\text {Putting the value of v}, \text {we get : } \]
\[\sqrt{\left( \frac{Rg}{2} \right)^2} = Rg\cos\theta\]
\[ \Rightarrow \frac{Rg}{2} = Rg\cos\theta\]
\[ \Rightarrow \cos\theta = \frac{1}{2}\]
\[ \Rightarrow \theta = 60^\circ = \frac{\pi}{3}\]
\[ \because \theta = \frac{L}{R}\]
\[ \therefore L = R\theta = \frac{\pi R}{3}\]
So, it will lose contact at a distance \[\frac{\pi R}{3}\] from the highest point.
(c) Let the uniform speed on the bridge be v. The chances of losing contact is maximum at the end bridge. We have :
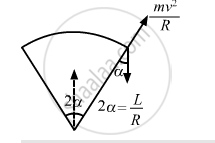
\[\alpha = \frac{L}{2R}\]
\[\text{So}, \frac{\text{mv}^2}{R} = \text{mg}\cos\alpha\]
\[ \Rightarrow v = \sqrt{\text{gRcos}\left( \frac{L}{2R} \right)}\]
APPEARS IN
RELATED QUESTIONS
A particle is kept fixed on a turntable rotating uniformly. As seen from the ground the particle goes in a circle, its speed is 20 cm/s and acceleration is 20 cm/s2. The particle is now shifted to a new position to make the radius half of the original value. The new value of the speed and acceleration will be
A motorcycle is going on an overbridge of radius R. The driver maintains a constant speed. As the motorcycle is ascending on the overbridge, the normal force on it
A simple pendulum having a bob of mass m is suspended from the ceiling of a car used in a stunt film shooting. the car moves up along an inclined cliff at a speed v and makes a jump to leave the cliff and lands at some distance. Let R be the maximum height of the car from the top of the cliff. The tension in the string when the car is in air is
An object follows a curved path. The following quantities may remain constant during the motion
(a) speed
(b) velocity
(c) acceleration
(d) magnitude of acceleration.
The position vector of a particle in a circular motion about the origin sweeps out equal area in equal time. Its
(a) velocity remains constant
(b) speed remains constant
(c) acceleration remains constant
(d) tangential acceleration remains constant.
A particle is going in a spiral path as shown in figure with constant speed.
A car of mass M is moving on a horizontal circular path of radius r. At an instant its speed is v and is increasing at a rate a.
(a) The acceleration of the car is towards the centre of the path.
(b) The magnitude of the frictional force on the car is greater than \[\frac{\text{mv}^2}{\text{r}}\]
(c) The friction coefficient between the ground and the car is not less than a/g.
(d) The friction coefficient between the ground and the car is \[\mu = \tan^{- 1} \frac{\text{v}^2}{\text{rg}.}\]
A stone is fastened to one end of a string and is whirled in a vertical circle of radius R. Find the minimum speed the stone can have at the highest point of the circle.
A mosquito is sitting on an L.P. record disc rotating on a turn table at \[33\frac{1}{3}\] revolutions per minute. The distance of the mosquito from the centre of the turn table is 10 cm. Show that the friction coefficient between the record and the mosquito is greater than π2/81. Take g =10 m/s2.
A person stands on a spring balance at the equator. By what fraction is the balance reading less than his true weight?
A car goes on a horizontal circular road of radius R, the speed increasing at a constant rate \[\frac{\text{dv}}{\text{dt}} = a\] . The friction coefficient between the road and the tyre is μ. Find the speed at which the car will skid.
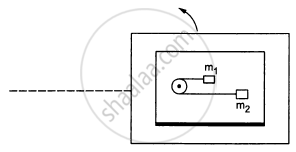
A table with smooth horizontal surface is placed in a circle of a large radius R (In the following figure). A smooth pulley of small radius is fastened to the table. Two masses m and 2m placed on the table are connected through a string going over the pulley. Initially the masses are held by a person with the string along the outward radius and then the system is released from rest (with respect to the cabin). Find the magnitude of the initial acceleration of the masses as seen from the cabin and the tension in the string.
A wheel is subjected to uniform angular acceleration about its axis. The wheel is starting from rest and it rotates through an angle θ1, in first two seconds. In the next two seconds, it rotates through an angle θ2. The ratio θ1/θ2 is ____________.
A child starts running from rest along a circular track of radius r with constant tangential acceleration a. After time the feels that slipping of shoes on the ground has started. The coefficient of friction between shoes and the ground is [g = acceleration due to gravity].
Angular displacement (θ) of a flywheel varies with time as θ = at + bt2 + ct3 then angular acceleration is given by ____________.
If a cyclist doubles his speed while negotiating a curve, how does the tendency to overturn vary?
An engine is moving on a c1rcular path of radius 200 m with speed of 15 m/s. What will be the frequency heard by an observer who is at rest at the centre of the circular path, when engine blows the whistle with frequency 250 Hz?
When a body slides down from rest along a smooth inclined plane making an angle of 45° with the horizontal, it takes time T. When the same body slides down from rest along a rough inclined plane making the same angle and through the same distance, it is seen to take time pT, where p is some number greater than 1. Calculate the co-efficient of friction between the body and the rough plane.
Which of the following statements is FALSE for a particle moving in a circle with a constant angular speed?
