Advertisements
Advertisements
Question
A particle is kept fixed on a turntable rotating uniformly. As seen from the ground the particle goes in a circle, its speed is 20 cm/s and acceleration is 20 cm/s2. The particle is now shifted to a new position to make the radius half of the original value. The new value of the speed and acceleration will be
Options
10 cm/s, 10 cm/s2
10 cm/s, 80 cm/s2
40 cm/s, 10 cm/s2
40 cm/s, 40 cm/s2
Solution
(a) 10 cm/s, 10 cm/s2
It is given that the turntable is rotating with uniform angular velocity. Let the velocity be \[\omega\] .
We have:
\[\text{v = r}\omega\]
\[ \Rightarrow \text{v} \propto \text{r} (\text{P for constant }\omega)\]
\[\frac{v}{v'} = \frac{r}{r'}\]
\[ \Rightarrow \text{v}' = \frac{\text{v}}{2} = 10 \text{ cm/s}\]
Similarly, we have: \[a' = \frac{a}{2} = 10\text{ cm/ s}^2\]
APPEARS IN
RELATED QUESTIONS
A stone of mass m tied to a string of length l is rotated in a circle with the other end of the string as the centre. The speed of the stone is v. If the string breaks, the stone will move
A coin placed on a rotating turntable just slips. If it is placed at a distance of 4 cm from the centre. If the angular velocity of the turntable is doubled, it will just slip at a distance of
Assume that the earth goes round the sun in a circular orbit with a constant speed of 30 kms
A stone is fastened to one end of a string and is whirled in a vertical circle of radius R. Find the minimum speed the stone can have at the highest point of the circle.
A ceiling fan has a diameter (of the circle through the outer edges of the three blades) of 120 cm and rpm 1500 at full speed. Consider a particle of mass 1 g sticking at the outer end of a blade. How much force does it experience when the fan runs at full speed? Who exerts this force on the particle? How much force does the particle exert on the blade along its surface?
A turn of radius 20 m is banked for the vehicles going at a speed of 36 km/h. If the coefficient of static friction between the road and the tyre is 0.4, what are the possible speeds of a vehicle so that it neither slips down nor skids up?
A car goes on a horizontal circular road of radius R, the speed increasing at a constant rate \[\frac{\text{dv}}{\text{dt}} = a\] . The friction coefficient between the road and the tyre is μ. Find the speed at which the car will skid.
A person stands on a spring balance at the equator. If the speed of earth's rotation is increased by such an amount that the balance reading is half the true weight, what will be the length of the day in this case?
Choose the correct option.
Select correct statement about the formula (expression) of moment of inertia (M.I.) in terms of mass M of the object and some of its distance parameter/s, such as R, L, etc.
In a certain unit, the radius of gyration of a uniform disc about its central and transverse axis is `sqrt2.5`. Its radius of gyration about a tangent in its plane (in the same unit) must be ______.
In non-uniform circular motion, the ratio of tangential to radial acceleration is (r = radius, a = angular acceleration and v = linear velocity)
A body slides down a smooth inclined plane having angle θ and reaches the bottom with velocity v. If a body is a sphere, then its linear velocity at the bottom of the plane is
Two particles A and B are located at distances rA and rB respectively from the centre of a rotating disc such that rA > rB. In this case, if angular velocity ω of rotation is constant, then ______
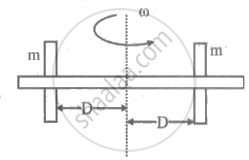
Two identical masses are connected to a horizontal thin (massless) rod as shown in the figure. When their distance from the pivot is D, a torque τ produces an angular acceleration of α1. The masses are now repositioned so that they are 2D from the pivot. The same torque produces an angular acceleration α2 which is given by ______
The real force 'F' acting on a particle of mass ' m' performing circular motion acts along the radius of circle 'r' and is directed towards the centre of circle. The square root of the magnitude of such force is (T = periodic time).
A rigid body is rotating with angular velocity 'ω' about an axis of rotation. Let 'v' be the linear velocity of particle which is at perpendicular distance 'r' from the axis of rotation. Then the relation 'v = rω' implies that ______.
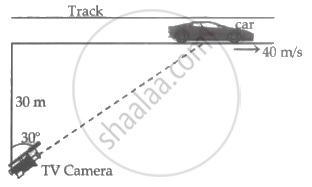
A racing car is travelling along a track at a constant speed of 40 m/s. A T.V. cameraman is recording the event from a distance of 30 m directly away from the track as shown in the figure. In order to keep the car under view in the position shown, the angular speed with which the camera should be rotated is ______.
Which of the following statements is FALSE for a particle moving in a circle with a constant angular speed?
Define centripetal force.
