Question

A block of mass m is kept on a horizontal ruler. The friction coefficient between the ruler and the block is μ. The ruler is fixed at one end and the block is at a distance L from the fixed end. The ruler is rotated about the fixed end in the horizontal plane through the fixed end. (a) What can the maximum angular speed be for which the block does not slip? (b) If the angular speed of the ruler is uniformly increased from zero at an angular acceleration α, at what angular speed will the block slip? 

Answer 1

(a) Given:
Mass of the block = m
Friction coefficient between the ruler and the block = μ
Let the maximum angular speed be ω₁ for which the block does not slip
Now, for the uniform circular motion in the horizontal plane, we have : 

\[\mu \text{mg = m }\omega_1^2 L\]

\[ \therefore \omega_1 = \sqrt{\frac{\mu g}{L}}\]

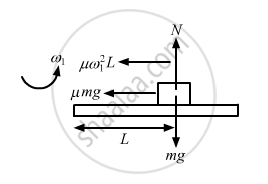
(b) Let the block slip at an angular speed ω_2. 
For the uniformly accelerated circular motion, we have :

\[\mu \text{mg} = \sqrt{\left( \text{ m }\omega_2^2 L \right)^2 + \left( \text{mL } \alpha^2 \right)^2}\]

\[ \Rightarrow \omega_2^4 + \alpha^2 = \frac{\mu^2 g^2}{L^2}\]

\[\mu \text{mg } = \sqrt{\left( \text{ m }\omega_2^2 L \right)^2 + \left( \text{ mL } \alpha^2 \right)^2}\]

\[ \Rightarrow \omega_2^4 + \alpha^2 = \frac{\mu^2 g^2}{L^2}\]

\[\Rightarrow \omega_2 = \left[ \left( \frac{\mu g}{L} \right)^2 - \alpha^2 \right]^{1/4}\]