Advertisements
Advertisements
Question
A disc revolves with a speed of `33 1/3` rev/min, and has a radius of 15 cm. Two coins are placed at 4 cm and 14 cm away from the centre of the record. If the co-efficient of friction between the coins and the record is 0.15, which of the coins will revolve with the record?
Solution 1
If the coin is to revolve with the record, then the force of friction must be enough to provide the necessary centripetal force
`:. mr omega^2 <= mu_s mg` or `r <= (mu_s mg)/(m omega^2)` or `r <= (mu_sg)/omega^2`
frequency = `33 1/2 "rpm"` = `100/3 "rpm" = 100/(3xx60) "rps"`
The Problems in which centripetal force is obtained fromforce of friction, start with the follwoing equation:
`m romega^2 <= mu_s mg`
`omega = 2pi xx 100/(3xx60)"rad s"^(-1) = 10/9 pi rad s^(-1)`
`(mu_sg)/omega^2 = (0.15xx10)/(10/9 pi)^2 m = 0.12 m = 12 cm`
The condition (r < = 12 cm) is satified by the coin placed at 4 cm from the centre of record. So the coin at 4 cm will revolve with the record.
Solution 2
Coin placed at 4 cm from the centre
Mass of each coin = m
Radius of the disc, r = 15 cm = 0.15 m
Frequency of revolution, v = `33 1/3` rev/min = `100/ (3xx60) = 5/9 "rev/s"`
Coefficient of friction, μ = 0.15
In the given situation, the coin having a force of friction greater than or equal to the centripetal force provided by the rotation of the disc will revolve with the disc. If this is not the case, then the coin will slip from the disc.
Coin placed at 4 cm:
Radius of revolution, r' = 4 cm = 0.04 m
Angular frequency, ω = 2πν = `2 xx 22/7 xx 5/9 = 3.49 s^(-1)`
Frictional force, f = μmg = 0.15 × m × 10 = 1.5m N
Centripetal force on the coin:
`F_"cent" = mr^'omega^2`
`= m xx 0.04 xx (3.49)^2`
= 0.49 m N
Since f > Fcent, the coin will revolve along with the record.
Coin placed at 14 cm:
Radius, `r^n` = 14 cm = 0.14 m
Angular frequency, ω = 3.49 s–1
Frictional force, f' = 1.5m N
Centripetal force is given as:
`F_"cent" = mr^"` `omega^2`
= m × 0.14 × (3.49)2
= 1.7m N
Since f < Fcent., the coin will slip from the surface of the record.
APPEARS IN
RELATED QUESTIONS
A rod of length L is pivoted at one end and is rotated with a uniform angular velocity in a horizontal plane. Let T1 and T2 be the tensions at the points L/4 and 3L/4 away from the pivoted ends.
Find the acceleration of the moon with respect to the earth from the following data:
Distance between the earth and the moon = 3.85 × 105 km and the time taken by the moon to complete one revolution around the earth = 27.3 days.
A mosquito is sitting on an L.P. record disc rotating on a turn table at \[33\frac{1}{3}\] revolutions per minute. The distance of the mosquito from the centre of the turn table is 10 cm. Show that the friction coefficient between the record and the mosquito is greater than π2/81. Take g =10 m/s2.
Suppose the amplitude of a simple pendulum having a bob of mass m is θ0. Find the tension in the string when the bob is at its extreme position.
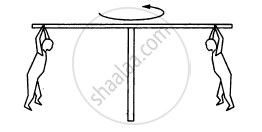
In a children's park a heavy rod is pivoted at the centre and is made to rotate about the pivot so that the rod always remains horizontal. Two kids hold the rod near the ends and thus rotate with the rod (In the following figure). Let the mass of each kid be 15 kg, the distance between the points of the rod where the two kids hold it be 3.0 m and suppose that the rod rotates at the rate of 20 revolutions per minute. Find the force of friction exerted by the rod on one of the kids.
A hemispherical bowl of radius R is rotated about its axis of symmetry which is kept vertical. A small block is kept in the bowl at a position where the radius makes an angle θ with the vertical. The block rotates with the bowl without any slipping. The friction coefficient between the block and the bowl surface is μ. Find the range of the angular speed for which the block will not slip.
A body is moving along a circular track of radius 100 m with velocity 20 m/s. Its tangential acceleration is 3 m/s2 then its resultant accelaration will be ______.
An engine is moving on a c1rcular path of radius 200 m with speed of 15 m/s. What will be the frequency heard by an observer who is at rest at the centre of the circular path, when engine blows the whistle with frequency 250 Hz?
A stone tide to a string of length L is whirled in a vertical circle with the other end of the string at the centre. At a certain instant of time, the stone is at its lowest position and has a speed u. The magnitude of change in its velocity, as it reaches a position where the string is horizontal, is `sqrt(x("u"^2 - "gL")`. The value of x is ______.
Statement I: A cyclist is moving on an unbanked road with a speed of 7 kmh-1 and takes a sharp circular turn along a path of radius of 2 m without reducing the speed. The static friction coefficient is 0.2. The cyclist will not slip and pass the curve. (g = 9.8 m/s2)
Statement II: If the road is banked at an angle of 45°, cyclist can cross the curve of 2 m radius with the speed of 18.5 kmh-1 without slipping.
In the light of the above statements, choose the correct answer from the options given below.
