Advertisements
Advertisements
Question
The rear side of a truck is open and a box of 40 kg mass is placed 5 m away from the open end as shown in Figure. The coefficient of friction between the box and the surface below it is 0.15. On a straight road, the truck starts from rest and accelerates with 2 m s–2. At what distance from the starting point does the box fall off the truck? (Ignore the size of the box).
Advertisements
Solution 1
Force experienced by box, F = ma = 40 x 2 = 80 N
Frictional force `F_f = mu mg` = 0.15 x 40 x 10 = 60 N.
Backward acceleration produced in the box, `a =20/40("Net Force")/m`
`=>a = 0.5 "ms"^(-2)`
if t is time taken by the box to travel s =5 metre and fall off the truck, then from
`S = ut + 1/2 at^2`
`5 = 0 xx t + 1/2 xx 0.5 t^2`
`t= sqrt((5xx2)/0.5) = 4.47 s`
if the truck travel a distace x during this time, then again from
`S = ut + 1/2 at^2`
`x = 0 xx 4.47 + 1/2 xx 2(4.47)^2 = 19.98 m`
Solution 2
Mass of the box, m = 40 kg
Coefficient of friction, μ = 0.15
Initial velocity, u = 0
Acceleration, a = 2 m/s2
Distance of the box from the end of the truck, s' = 5 m
As per Newton’s second law of motion, the force on the box caused by the accelerated motion of the truck is given by: F = ma
= 40 × 2 = 80 N
As per Newton’s third law of motion, a reaction force of 80 N is acting on the box in the backward direction. The backward motion of the box is opposed by the force of friction f, acting between the box and the floor of the truck. This force is given by:
f = μmg
= 0.15 × 40 × 10 = 60 N
∴Net force acting on the block:
Fnet = 80 – 60 = 20 N backward
The backward acceleration produced in the box is given by:
`a_"back" = F_"net"/m = 20/ 4 = 0.5 "m/s"^2`
Using the second equation of motion, time t can be calculated as:
`s' = ut + 1/2 a_"back" t^2`
`5 = 0 + 1/2 xx 0.5 xx t^2`
`:.t = sqrt20 s`
Hence, the box will fall from the truck after `sqrt20 s` from start
The distance s, travelled by the truck in `sqrt20 s` is given by the relation:
`s = ut + 1/2 at^2`
`=0 + 1/2xx2 xx(sqrt20)^2`
= 20 m
RELATED QUESTIONS
The below figure shows the position-time graph of a particle of mass 4 kg.
- What is the force on the particle for t < 0, t > 4 s, 0 < t < 4 s?
- What is the impulse at t = 0 and t = 4 s? (Consider one-dimensional motion only.)
An aircraft executes a horizontal loop at a speed of 720 km/h with its wings banked at 15°. What is the radius of the loop?
A block of mass 15 kg is placed on a long trolley. The coefficient of static friction between the block and the trolley is 0.18. The trolley accelerates from rest with 0.5 ms–2 for 20 s and then moves with uniform velocity. Discuss the motion of the block as viewed by (a) a stationary observer on the ground, (b) an observer moving with the trolley.
A spy jumps from an airplane with his parachute. The spy accelerates downward for some time when the parachute opens. The acceleration is suddenly checked and the spy slowly falls to the ground. Explain the action of the parachute in checking the acceleration.
Both the springs shown in the following figure are unstretched. If the block is displaced by a distance x and released, what will be the initial acceleration?
The force of buoyancy exerted by the atmosphere on a balloon is B in the upward direction and remains constant. The force of air resistance on the balloon acts opposite the direction of velocity and is proportional to it. The balloon carries a mass M and is found to fall to the earth's surface with a constant velocity v. How much mass should be removed from the balloon so that it may rise with a constant velocity v?
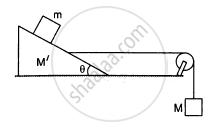
Find the mass M of the hanging block in the following figure that will prevent the smaller block from slipping over the triangular block. All the surfaces are frictionless and the strings and the pulleys are light.
A monkey is climbing on a rope that goes over a smooth light pulley and supports a block of equal mass at the other end in the following figure. Show that whatever force the monkey exerts on the rope, the monkey and the block move in the same direction with equal acceleration. If initially both were at rest, their separation will not change as time passes.
In the following figure shows a man of mass 60 kg standing on a light weighing machine kept in a box of mass 30 kg. The box is hanging from a pulley fixed to the ceiling by a light rope, the other end of which is held by the man himself. If the man manages to keep the box at rest, what is the weight recorded on the machine? What force should he exert on the rope to record his correct weight on the machine?
The linear momentum of a body of mass m moving with velocity v is :
The linear momentum of a ball of mass 50 g is 0.5 kg m s-1. Find its velocity.
A car is moving with a uniform velocity 30 ms-1. It is stopped in 2 s by applying a force of 1500 N through its brakes. Calculate the following values : The change in momentum of car.
A ball is thrown vertically upwards. It returns 6 s later. Calculate the greatest height reached by the ball. (Take g = 10 m s−2)
Prove mathematically F = ma
What do you mean by linear momentum of a body?
State Newton's second law of motion. Is Newton's first law of motion contained in Newton's second law of motion?
Use Newton's second law to explain the following:
We always prefer to land on sand instead of hard floor while taking a high jump.
Why does a child feel more pain when she falls down on a hard cement floor, than when she falls on the soft muddy ground in the garden?
How does moving your hand backward while catching a cricket ball reduce pain?
