Advertisements
Advertisements
Question
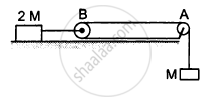
Find the acceleration of the 500 g block in the following figure.
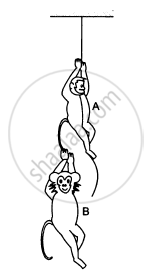
Solution
Given,
m1 = 100 g = 0.1 kg
m2 = 500 g = 0.5 kg
m3 = 50 g = 0.05 kg
The free-body diagram for the system is shown below: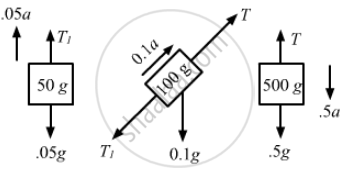
From the free-body diagram of the 500 g block,
T + 0.5a − 0.5g = 0 .....(i)
From the free-body diagram of the 50 g block,
T1 + 0.05g − 0.05a = a ....(ii)
From the free-body diagram of the 100 g block,
T1 + 0.1a − T + 0.5g = 0 ....(iii)
From equation (ii),
T1 = 0.05g + 0.05a .....(iv)
From equation (i),
T1 = 0.5g − 0.5a .....(v)
Equation (iii) becomes
T1 + 0.1a − T + 0.05g = 0
From equations (iv) and (v), we get:
0.05g + 0.05a + 0.1a − 0.5g + 0.5a + 0.05g = 0
0.65a = 0.4 g
\[\Rightarrow a = \frac{0 . 4}{0 . 65}g\]
\[ = \frac{40}{65}g = \frac{8}{13}g \left(\text{ downward }\right)\]
So, the acceleration of the 500 gm block is
\[\frac{8g}{13}\] downward.
APPEARS IN
RELATED QUESTIONS
A constant retarding force of 50 N is applied to a body of mass 20 kg moving initially with a speed of 15 ms–1. How long does the body take to stop?
Explain why a cricketer moves his hands backwards while holding a catch.
A helicopter of mass 1000 kg rises with a vertical acceleration of 15 m s–2. The crew and the passengers weigh 300 kg. Give the magnitude and direction of the
(a) force on the floor by the crew and passengers,
(b) action of the rotor of the helicopter on the surrounding air,
(c) force on the helicopter due to the surrounding air.
In a TV picture tube, electrons are ejected from the cathode with negligible speed and they attain a velocity of 5 × 106 m/s in travelling one centimetre. Assuming straight-line motion, find the constant force exerted on the electrons. The mass of an electron is 9.1 × 10−31 kg.
Two blocks of equal mass m are tied to each other through a light string. One of the blocks is pulled along the line joining them with a constant force F. Find the tension in the string joining the blocks.
A particle of mass 50 g moves in a straight line. The variation of speed with time is shown in the following figure. Find the force acting on the particle at t = 2, 4 and 6 seconds.
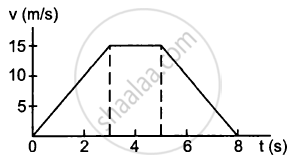
A particle of mass 0.3 kg is subjected to a force F = −kx with k = 15 N/m. What will be its initial acceleration if it is released from a point x = 20 cm?
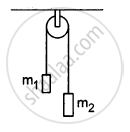
In a simple Atwood machine, two unequal masses m1 and m2 are connected by a string going over a clamped light smooth pulley. In a typical arrangement (In the following figure), m1 = 300 g and m2 = 600 g. The system is released from rest. (a) Find the distance travelled by the first block in the first two seconds; (b) find the tension in the string; (c) find the force exerted by the clamp on the pulley.
In the previous problem, suppose m2 = 2.0 kg and m3 = 3.0 kg. What should be the mass m, so that it remains at rest?
Consider the situation shown in the following figure. Both the pulleys and the string are light and all the surfaces are frictionless. (a) Find the acceleration of the mass M; (b) find the tension in the string; (c) calculate the force exerted by the clamp on the pulley A in the figure.
A block is kept on the floor of an elevator at rest. The elevator starts descending with an acceleration of 12 m/s2. Find the displacement of the block during the first 0.2 s after the start. Take g = 10 m/s2.
An aeroplane is moving uniformly at a constant height under the action of two forces (i) Upward force (lift) and (ii) Downward force (weight). What is the net force on the aeroplane?
Define linear momentum and state its S.I. unit.
A force acts for 10 s on a stationary body of mass 100 kg, after which the force ceases to act. The body moves through a distance of 100 m in the next 5 s. Calculate: The velocity acquired by the body.
Define Newton’s second law of motion.
A stone is thrown vertically upward with a velocity of 9.8 m/s. When will it reach the ground?
What do you mean by the conservation of momentum? Briefly, explain the collision between two bodies and the conservation of momentum.
A cricket ball of mass 150 g has an initial velocity `u = (3hati + 4hatj)` m s−1 and a final velocity `v = - (3hati + 4hatj)` m s−1 after being hit. The change in momentum (final momentum-initial momentum) is (in kg m s1)
The position time graph of a body of mass 2 kg is as given in figure. What is the impulse on the body at t = 0 s and t = 4 s.

