Advertisements
Advertisements
प्रश्न
Find the acceleration of the 500 g block in the following figure.
उत्तर
Given,
m1 = 100 g = 0.1 kg
m2 = 500 g = 0.5 kg
m3 = 50 g = 0.05 kg
The free-body diagram for the system is shown below: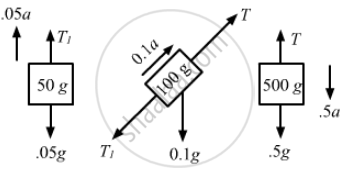
From the free-body diagram of the 500 g block,
T + 0.5a − 0.5g = 0 .....(i)
From the free-body diagram of the 50 g block,
T1 + 0.05g − 0.05a = a ....(ii)
From the free-body diagram of the 100 g block,
T1 + 0.1a − T + 0.5g = 0 ....(iii)
From equation (ii),
T1 = 0.05g + 0.05a .....(iv)
From equation (i),
T1 = 0.5g − 0.5a .....(v)
Equation (iii) becomes
T1 + 0.1a − T + 0.05g = 0
From equations (iv) and (v), we get:
0.05g + 0.05a + 0.1a − 0.5g + 0.5a + 0.05g = 0
0.65a = 0.4 g
\[\Rightarrow a = \frac{0 . 4}{0 . 65}g\]
\[ = \frac{40}{65}g = \frac{8}{13}g \left(\text{ downward }\right)\]
So, the acceleration of the 500 gm block is
\[\frac{8g}{13}\] downward.
APPEARS IN
संबंधित प्रश्न
A body of mass 0.40 kg moving initially with a constant speed of 10 m s–1 to the north is subject to a constant force of 8.0 N directed towards the south for 30 s. Take the instant the force is applied to be t = 0, the position of the body at that time to be x = 0, and predict its position at t = –5 s, 25 s, 100 s.
A stone of mass m tied to the end of a string revolves in a vertical circle of radius R. The net forces at the lowest and highest points of the circle directed vertically downwards are: [Choose the correct alternative]
| Lowest Point | Highest Point | |
| a) | mg – T1 | mg + T2 |
| b) | mg + T1 | mg – T2 |
| c) | `mg + T1 –(m_v_1^2)/R` | mg – T2 + (`mv_1^2`)/R |
| d) | `mg – T1 – (mv)/R` | mg + T2 + (mv_1^2)/R |
T1 and v1 denote the tension and speed at the lowest point. T2 and v2 denote corresponding values at the highest point.
A block of mass 15 kg is placed on a long trolley. The coefficient of static friction between the block and the trolley is 0.18. The trolley accelerates from rest with 0.5 ms–2 for 20 s and then moves with uniform velocity. Discuss the motion of the block as viewed by (a) a stationary observer on the ground, (b) an observer moving with the trolley.
Suppose you are running fast in a field and suddenly find a snake in front of you. You stop quickly. Which force is responsible for your deceleration?
A free 238U nucleus kept in a train emits an alpha particle. When the train is stationary, a nucleus decays and a passenger measures that the separation between the alpha particle and the recoiling nucleus becomes x at time t after the decay. If the decay takes place while the train is moving at a uniform velocity v, the distance between the alpha particle and the recoiling nucleus at a time t after the decay, as measured by the passenger, is
The figure shows the displacement of a particle going along the X-axis as a function of time. The force acting on the particle is zero in the region
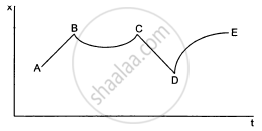
(a) AB
(b) BC
(c) CD
(d) DE
The force of buoyancy exerted by the atmosphere on a balloon is B in the upward direction and remains constant. The force of air resistance on the balloon acts opposite the direction of velocity and is proportional to it. The balloon carries a mass M and is found to fall to the earth's surface with a constant velocity v. How much mass should be removed from the balloon so that it may rise with a constant velocity v?
An empty plastic box of mass m is found to accelerate up at the rate of g/6 when placed deep inside water. How much sand should be put inside the box so that it may accelerate down at the rate of g/6?
A force \[\vec{F} = \vec{v} \times \vec{A}\] is exerted on a particle in addition to the force of gravity, where \[\vec{v}\] is the velocity of the particle and \[\vec{A}\] is a constant vector in the horizontal direction. With what minimum speed, a particle of mass m be projected so that it continues to move without being defelected and with a constant velocity?
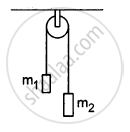
In a simple Atwood machine, two unequal masses m1 and m2 are connected by a string going over a clamped light smooth pulley. In a typical arrangement (In the following figure), m1 = 300 g and m2 = 600 g. The system is released from rest. (a) Find the distance travelled by the first block in the first two seconds; (b) find the tension in the string; (c) find the force exerted by the clamp on the pulley.
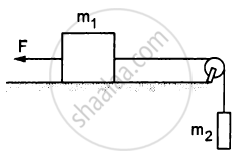
A constant force F = m2g/2 is applied on the block of mass m1 as shown in the following figure. The string and the pulley are light and the surface of the table is smooth. Find the acceleration of m1.
A block is kept on the floor of an elevator at rest. The elevator starts descending with an acceleration of 12 m/s2. Find the displacement of the block during the first 0.2 s after the start. Take g = 10 m/s2.
Define linear momentum and state its S.I. unit.
A bullet of mass 50 g moving with an initial velocity 100 m s-1 strikes a wooden block and comes to rest after penetrating a distance 2 cm in it. Calculate: (i) Initial momentum of the bullet, (ii) Final momentum of the bullet, (iii) Retardation caused by the wooden block and (iv) Resistive force exerted by the wooden block.
A ball is thrown vertically upwards. It returns 6 s later. Calculate : The greatest height reached by the ball . (Take g = 10 m s-2)
A pebble is dropped freely in a well from its top. It takes 20 s for the pebble to reach the water surface in the well. Taking g = 10 m s-2 and speed of sound = 330 m s-1. Find : The depth of water surface
Prove mathematically F = ma
ame the law of motion which gives the definition of force.
What do you mean by linear momentum of a body?
A ball is thrown upward and reaches a maximum height of 19.6 m. Find its initial speed?
