Advertisements
Advertisements
प्रश्न
Find the acceleration of the blocks A and B in the three situations shown in the following figure.

उत्तर
(a) 5a + T − 5g = 0
From free-body diagram (1),
T = 5g − 5a .....(i)
Again,
\[\left( \frac{1}{2} \right)T - 4g - 8a = 0\]
⇒ T − 8g − 16a = 0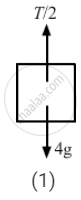
From free-body diagram (2),
T = 8g + 16a ......(ii)
From equations (i) and (ii), we get:
5g − 5a = 8g + 16a
\[\Rightarrow 21a = - 3g - a = - \frac{9}{7}\]
So, the acceleration of the 5 kg mass is \[\frac{9}{7} m/ s^2 \left(\text{ upward }\right)\] and that of the 4 kg mass is
\[2a = \frac{2g}{7} \left(\text{ downward }\right)\]
\[4a - \frac{T}{2} = 0\]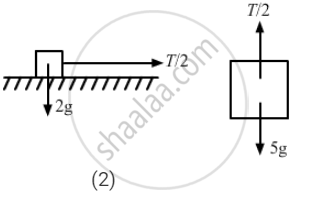
⇒ 8a − T = 0
⇒ T = 8a
Again, T + 5a − 5g = 0
From free body diagram-4,
8a + 5a − 5g = s0
⇒ 13a − 5g = 0
\[\Rightarrow a = \frac{5g}{13} \left(\text{ downward }\right)\]
Acceleration of mass 2 kg is \[2a = \frac{10}{13} \left( g \right)\] and 5 kg is
\[\frac{5g}{13}\].
(c) T + 1a − 1g = 0
From free body diagram-5
T = 1g − 1a .....(i)
Again, from free body diagram-6,
\[\frac{T}{2} - 2g - 4a = 0\]
⇒ T − 4g − 8a = 0 .....(ii)
From equation (i)
1g − 1a − 4g − 8a = 0
\[\Rightarrow a = \frac{g}{3}\left(\text{ downward }\right)\]
Acceleration of mass 1 kg is \[\frac{g}{3} \left(\text{ upward }\right)\]
Acceleration of mass 2 kg is \[\frac{2g}{3} \left(\text{ downward }\right)\] 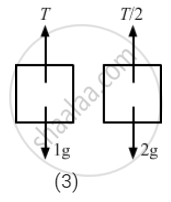
APPEARS IN
संबंधित प्रश्न
An aircraft executes a horizontal loop at a speed of 720 km/h with its wings banked at 15°. What is the radius of the loop?
A person drops a coin. Describe the path of the coin as seen by the person if he is in (a) a car moving at constant velocity and (b) in a free falling elevator.
When a horse pulls a cart, the force that helps the horse to move forward is the force exerted by
If the tension in the cable supporting an elevator is equal to the weight of the elevator, the elevator may be
(a) going up with increasing speed
(b) going down with increasing speed
(c) going up with uniform speed
(d) going down with uniform speed
Suppose the ceiling in the previous problem is that of an elevator which is going up with an acceleration of 2.0 m/s2. Find the elongation.
Find the acceleration of the 500 g block in the following figure.
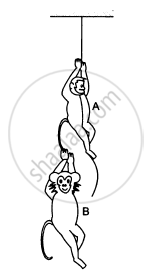
In the following figure shows a man of mass 60 kg standing on a light weighing machine kept in a box of mass 30 kg. The box is hanging from a pulley fixed to the ceiling by a light rope, the other end of which is held by the man himself. If the man manages to keep the box at rest, what is the weight recorded on the machine? What force should he exert on the rope to record his correct weight on the machine?
Write the mathematical form of Newton's second law of motion. State the conditions if any.
Use Newton's second law of motion to explain the following instance :
An athlete prefers to land on sand instead of hard floor while taking a high jump .
The unit of linear momentum is :
The linear momentum of a body of mass m moving with velocity v is :
A force of 10 N acts on a body of mass 2 kg for 3 s, initially at rest. Calculate : Change in momentum of the body.
A bullet of mass 50 g moving with an initial velocity 100 m s-1 strikes a wooden block and comes to rest after penetrating a distance 2 cm in it. Calculate: (i) Initial momentum of the bullet, (ii) Final momentum of the bullet, (iii) Retardation caused by the wooden block and (iv) Resistive force exerted by the wooden block.
Multiple Choice Question. Select the correct option.
The impulse of a body is equal to:
Use Newton's second law to explain the following:
We always prefer to land on sand instead of hard floor while taking a high jump.
A stone is dropped from a cliff 98 m high.
What will be its speed when it strikes the ground?
What do you mean by the conservation of momentum? Briefly, explain the collision between two bodies and the conservation of momentum.
The INCORRECT statement about Newton's second law of motion is
A hockey player is moving northward and suddenly turns westward with the same speed to avoid an opponent. The force that acts on the player is ______.
