Advertisements
Advertisements
Question
Find the acceleration of the blocks A and B in the three situations shown in the following figure.

Solution
(a) 5a + T − 5g = 0
From free-body diagram (1),
T = 5g − 5a .....(i)
Again,
\[\left( \frac{1}{2} \right)T - 4g - 8a = 0\]
⇒ T − 8g − 16a = 0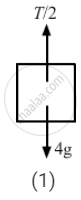
From free-body diagram (2),
T = 8g + 16a ......(ii)
From equations (i) and (ii), we get:
5g − 5a = 8g + 16a
\[\Rightarrow 21a = - 3g - a = - \frac{9}{7}\]
So, the acceleration of the 5 kg mass is \[\frac{9}{7} m/ s^2 \left(\text{ upward }\right)\] and that of the 4 kg mass is
\[2a = \frac{2g}{7} \left(\text{ downward }\right)\]
\[4a - \frac{T}{2} = 0\]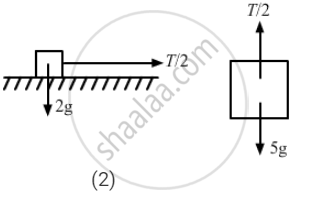
⇒ 8a − T = 0
⇒ T = 8a
Again, T + 5a − 5g = 0
From free body diagram-4,
8a + 5a − 5g = s0
⇒ 13a − 5g = 0
\[\Rightarrow a = \frac{5g}{13} \left(\text{ downward }\right)\]
Acceleration of mass 2 kg is \[2a = \frac{10}{13} \left( g \right)\] and 5 kg is
\[\frac{5g}{13}\].
(c) T + 1a − 1g = 0
From free body diagram-5
T = 1g − 1a .....(i)
Again, from free body diagram-6,
\[\frac{T}{2} - 2g - 4a = 0\]
⇒ T − 4g − 8a = 0 .....(ii)
From equation (i)
1g − 1a − 4g − 8a = 0
\[\Rightarrow a = \frac{g}{3}\left(\text{ downward }\right)\]
Acceleration of mass 1 kg is \[\frac{g}{3} \left(\text{ upward }\right)\]
Acceleration of mass 2 kg is \[\frac{2g}{3} \left(\text{ downward }\right)\] 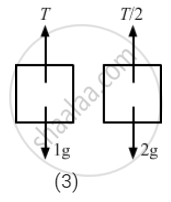
APPEARS IN
RELATED QUESTIONS
An aircraft executes a horizontal loop at a speed of 720 km/h with its wings banked at 15°. What is the radius of the loop?
A free 238U nucleus kept in a train emits an alpha particle. When the train is stationary, a nucleus decays and a passenger measures that the separation between the alpha particle and the recoiling nucleus becomes x at time t after the decay. If the decay takes place while the train is moving at a uniform velocity v, the distance between the alpha particle and the recoiling nucleus at a time t after the decay, as measured by the passenger, is
The figure shows the displacement of a particle going along the X-axis as a function of time. The force acting on the particle is zero in the region
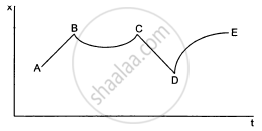
(a) AB
(b) BC
(c) CD
(d) DE
car moving at 40 km/hr is to be stopped by applying brakes in the next 4 m. If the car weighs 2000 kg, what average force must be applied to stop it?
A man has fallen into a ditch of width d and two of his friends are slowly pulling him out using a light rope and two fixed pulleys as shown in the following figure. Show that the force (assumed equal for both the friends) exerted by each friend on the road increases as the man moves up. Find the force when the man is at a depth h.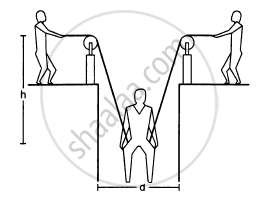
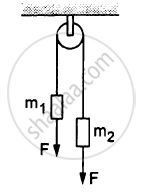
In the following figure, m1 = 5 kg, m2 = 2 kg and F = 1 N. Find the acceleration of either block. Describe the motion of m1 if the string breaks but F continues to act.
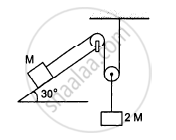
Find the acceleration of the block of mass M in the situation shown in the following figure. All the surfaces are frictionless and the pulleys and the string are light.
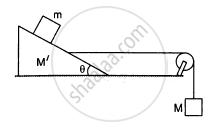
Find the mass M of the hanging block in the following figure that will prevent the smaller block from slipping over the triangular block. All the surfaces are frictionless and the strings and the pulleys are light.
Two balls A and B of masses m and 2 m are in motion with velocities 2v and v, respectively. Compare:
(i) Their inertia.
(ii) Their momentum.
(iii) The force needed to stop them in the same time.
Use Newton's second law of motion to explain the following instance :
A cricketer pulls his hands back while catching a fast moving cricket ball .
Use Newton's second law of motion to explain the following instance :
An athlete prefers to land on sand instead of hard floor while taking a high jump .
A body of mass 5 kg is moving with velocity 2 m s-1. Calculate its linear momentum.
How long will a stone take to fall to the ground from the top of a building 80 m high
A pebble is dropped freely in a well from its top. It takes 20 s for the pebble to reach the water surface in the well. Taking g = 10 m s-2 and speed of sound = 330 m s-1. Find : The depth of water surface
A motorcycle of mass 100 kg is running at 10 ms−1. If its engine develops an extra linear momentum of 2000 Ns, calculate the new velocity of a motorcycle.
Name the physical entity used for quantifying the motion of a body.
State Newton's second law of motion.
A body of mass 400 g is resting on a frictionless table. Find the acceleration of the body when acted upon by a force of 0.02 N.
Use Newton's second law to explain the following:
We always prefer to land on sand instead of hard floor while taking a high jump.
What do you mean by the conservation of momentum? Briefly, explain the collision between two bodies and the conservation of momentum.
